Einführung des Motors Betriebsprinzip:
Das Betriebsprinzip des Induktionsmotors in Abbildung 9.4 zeigt die Querschnittsansicht eines Induktionsmotors. Der Stator wird von einer Dreiphasen-V / Phase-Spannungsnetzversorgung und Frequenz F Hz angetrieben. Der Rotor ist in 3 Phasen für so viele Pole wie der Stator verwundet und ist kurzübertragbar. Es wird angenommen, dass der Widerstand des Stators und die Reaktanz der Lecks für beide vernachlässigbar sind
![]()
Oder
- E1 = EMF durch das Stator / die Phase induziert
- KW1 = Statorwicklungsfaktor
- NPH1 (Serie) = Stator Tourne / Phase Series
- Φr = resultierende Durchfluss / Luftpol
Es wird aus der Gleichung aus gesehen. (9.1), dass unabhängig von den vorhandenen Lastbedingungen am Rotor φR der in der Luftwanderung festgelegte Strömung / Pol konstant ist und mit der für die Hypothese angewendeten Spannung verbunden ist.
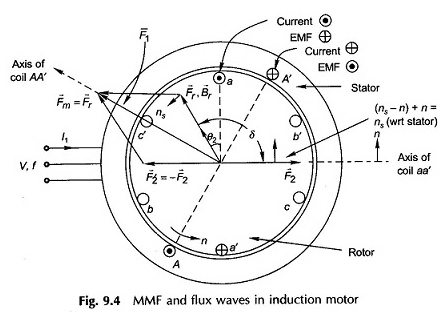
Der MMF -F̅R -Vektor mit dem B̅R -assoziierten Durchflussdichtevektor, der für die Produktion von φR verantwortlich ist, läuft mit einer synchronen Geschwindigkeit aus, da er mit 3 vom Stator gezogenen 3 ausgewogenen 3 -Phasen -Strömen verbunden ist.
Die relative Geschwindigkeit zwischen B̅R und dem Rotor führt zur Induktion eines Strommusters im Kurzschlussrotor.
Das Drehmoment, das durch die Wechselwirkung von B̅R und die Ströme des Rotors durch das Gesetz von Lenz erzeugt wird, würde dazu neigen, den Rotor in Drehrichtung von B̅R zu bewegen, um die relative Geschwindigkeit zu verringern.
Der Motor ist daher selbstsemarisch und der Rotor erhält eine konstante Geschwindigkeit n n
Abbildung 9.4 zeigt die relative Position der Vektoren f̅r, b̅r (Luftversteifungsmmf und Durchflussdichte), F̅2 (Rotor MMF), bei der F̅r F̅2 durch den Winkel Δ = 90 ° + θ2 (Autotomobilwirkung) führt, θ2 ist der Winkel, unter dem der Rotor-Rotor-EMF.
Der Winkel θ2 ist jedoch sehr klein, da die Reaktanz des Rotors viel kleiner ist als der Widerstand gegen den Rotor. Der MMF -Statorvektor wird dann gegeben
![]()
befindet sich im Vektordiagramm. Solange das Diagramm gezogen wird, sind das Stator und die Rotorphase A (dargestellt in Form einer einzelnen Spule) maximal möglich. Der Leser kann den Standort der Vektoren aus der A -aktuellen Phase überprüfen, in der die richtige Regel angewendet wird.
Gleit- und Frequenz von Rotorströmen:
In Bezug auf Abbildung 9.4 ist leicht zu beobachten, dass sich B̅r mit der Geschwindigkeit (NS – N) in Bezug auf Rotortreiber (in Richtung B̅R) bewegt. Dies ist als Gleitgeschwindigkeit bekannt. Verschiebung ist definiert als
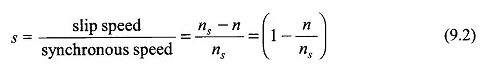
Offensichtlich s = 1 für n = 0, das heißt für den stationären Rotor und S = 0 für n = ns, dh für den Rotor, der mit einer synchronen Geschwindigkeit arbeitet.
Die Häufigkeit der im Rotor induzierten Ströme ist
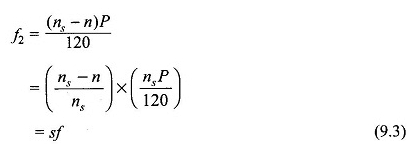
Der normale Ruf mit vollständiger Beladung des Betriebsprinzips des Induktionsmotors beträgt etwa 2% bis 8%, so dass die Frequenz der Rotorströme nur 1 bis 4 Hz beträgt.
Der Rotor durch EMF -Phase bei S = 1 (Schaltrotor) ist gegeben durch
![]()
Bei jeder Verschiebung wird die Frequenz des Rotors SF, die EMF durch den Rotor induziert, in SE2 umgewandelt. Betrachten Sie nun die Impedanz des Rotorkreises
![]()
Oder
- X2 = Rotorreaktanz des Rotors beim Stoppen (Rotorfrequenz = Statorfrequenz, f)
Wenn der Rotor bei Slip S arbeitet, ist seine Frequenz SF, seine Impedanz wird in verwandelt
![]()
Es wird daher festgestellt, dass die Frequenz der Rotorströme, ihre induzierte FEM und ihre Reaktanz in direktem Verhältnis zur Verschiebung variieren. Abbildung 9.5 zeigt den Rotorkreis mit Gleiten s. Der Schaltungsphasenwinkel ist

Produktion von MMF und Rotordrehmoment:
In Abbildung 9.4 als der Vektor der Durchflussdichte, der b̅r mit der Geschwindigkeit (ns – n) in Bezug auf den Rotor läuft, wird eine maximal positive EMF in der Rotorspule AA ‚(angezeigt durch Punkt im Treiber A angezeigt und im Treiber a‘), wenn B̅r bei 90 ° vor dem Rückgang liegt.
Da der Strom im Rotor hinter der EMF von θ2 zurückbleibt, ist der Strom in der Spule AA ‚maximal positiv, wenn B̅R durch den Winkel θ2 weiter vorgegangen ist. In diesem Moment wird der MMF -Vektor des Rotors F̅2 entlang der Achse der AA ‚Spule sein.
Es ist daher zu sehen, dass B̅r (oder F̅r) vor F̅2 in einem Winkel δ = (90 + θ2) liegt. Zusätzlich ist F̅2, das durch die Ströme des Frequenzrotors F2 = SF verursacht wird, im Vergleich zum Treiber des Rotors bei Geschwindigkeit (NS – N) und bei Geschwindigkeit ns.
In Bezug auf den Stator, weil sich der Rotor selbst mit der Geschwindigkeit n in die gleiche Richtung bewegt, im Vergleich zum Stator.
Somit bewegen sich F̅R und F̅2 beide mit einer synchronen Geschwindigkeit NS im Vergleich zum Stator und sind in Bezug auf die anderen mit F̅R, die sich vor F̅2 im Winkel befinden (90 ° + θ2), stationär.
Die Wechselwirkung des Rotorfeldes und des resultierenden Feldes erzeugt ein Paar in der Rotationsrichtung von f̅r.
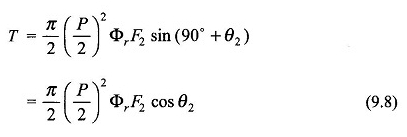
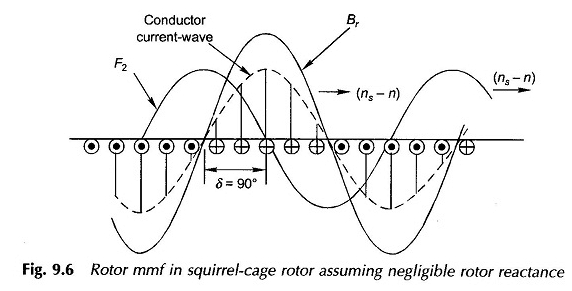
Betrachten Sie nun den Fall des Rotors des Eichhörnchens mit Treibern gleichmäßig um die Peripherie des Rotors. Die Reaktion des Rotor -MMF F2 wird besser aus dem entwickelten Diagramm von Fig. 1 visualisiert.
9.6, in dem sich der Rotor als stationär und die braune Welle vorgestellt hat – bewegt sich im Vergleich dazu bei der Schiebergeschwindigkeit (NS – N). Dass die Rotorreaktanz als vernachlässigbar angesehen wird, so dass die Fahrerströme (kurzübergegeben) mit dem EMF-Treiber übereinstimmen.
Das aktuelle Muster des Fahrers wird daher sinusal verteilt und befindet sich in der räumlichen Phase mit kurzer und bewegt sich synchron. Die Rotor -MMF -Welle ist eine gespeicherte Sinusus mit der gleichen Anzahl von Polen wie die Bewegung der rohen Welle.
Sein grundlegender (F2) in Abbildung 9.6 der Gesetze des BRs behauptet um 90 °. Wenn die Reaktanz des Rotors jetzt inszeniert wird, würde die Stromwelle des Fahrers und daher die Rotor -MMF -Welle durch Winkel θ2 zu spät sein.
Somit wäre der Winkel zwischen BR und der F2 -Welle (90 ° + θ2), die gleiche wie im Rotor der Wunde.
Ein Eichhörnchen -Zylinderrotor reagiert daher auf die gleiche Weise wie ein Wundrotor, außer dass die Anzahl der Phasen nicht offensichtlich ist – es kann als so viele Phasen angesehen werden wie die Balken / Pole. Ein Eichhörnchen-Rotor kann immer durch einen äquivalenten Wundrotor mit drei Phasen ersetzt werden.
Es wird aus der Gleichung aus gesehen. (9.8) als ein niedriger Reaktionsrotor (schwach θ2 = tan-1 jsx2 / r2) erzeugt ein größeres Paar für φR, F2 und S.
Ein Käfig -Eichhörnchenmotor ist in dieser Hinsicht im Vergleich zu einem Motor des Wundrotors höher, da der Käfigrotor eine niedrigere Reaktanz aufweist, da er keinen Überhang der Wicklung hat.
Eine sehr wichtige Beobachtung, die im Prinzip des Betriebs des Induktionsmotors hier gemacht werden kann, ist, dass die durch sie verursachten MMF (F2), obwohl die Rotorströme eine SF -Frequenz aufweisen, im Vergleich zum Stator mit einer synchronen Geschwindigkeit funktioniert.
Mit anderen Worten, die Reaktion der Rotorströme entspricht den Frequenzströmen (f) des Stators, die auf einem stationären zylindrischen Struktur entsprechen, das in den Stator anstelle des Rotors platziert ist.
Um sich auf eine andere Weise auszudrücken, haben die Ansichten der Rotorströme des Stators die Frequenz F, haben jedoch den gleichen RMS -Wert.
Der MMF -Stator F̅1 -Vektor befindet sich in Abbildung 9.4 der Vektorgleichung
![]()
Zusätzlich kann F̅1 in Komponenten unterteilt werden
![]()
wobei F̅2 gegen F̅2 und gleich der Größe und gleich ist und der Größe und gleich
![]()
Der Statorstrom, der F̅1 führt, entspricht dem EQ -Vektor. (9.10) in Komponenten unterteilt werden
![]()
Hier kann I̅M als Magnetisierungsstrom der Datei erkannt werden, der die mmf FR resultiert und die resultierende Strömung / Pol φR, während die Komponente des Statorstroms, die die Reaktion F2 des Rotors I2 ausbalanciert, ausbalanciert.
Abbildung 9.4 zeigt auch die relative Position der Stator AA ‚Spule und die positive Richtung des Stroms. Dieses sofortige Vektorbild gilt, wenn I2 einen maximalen positiven Wert hat.
Damit F’2 F2 absagt, muss die Statorstromkomponente, die den MMF -Rotor ausbalanciert, mit dem im Stator gezeigten Rotor -Strom übereinstimmen.
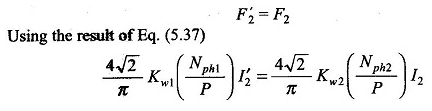

In Bezug auf Amplituden ist F’2 gegenüber F2 entgegengesetzt, so dass sie absagen, während ich 2 und I2 der Verhältnismäßigkeit der Gleichung befolgen müssen. (9.13) und muss in Phase sein.
Darüber hinaus können wir unter Bezugnahme auf Abbildung 9.4 leicht erkennen, dass im Stator die positive Richtung der EMF E1 der positiven Richtung von i1 entgegengesetzt ist, während im Rotor die positive Richtung von I2 in die positive Richtung von SE2 ist. Dies ähnelt dem Fall des Transformators.
Mit der Richtung eines positiven Stroms im Stator AA ‚Coil, der wie in Abbildung 9.4 gekennzeichnet ist, und die Richtung der Achse des Kolloquiums, das angegeben ist
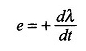
Dieses Betriebsprinzip des Induktionsmotors hat das gleiche Vorzeichen wie das, das im Transformatorgehäuse verwendet wird, so dass die φR -Durchflussphase und der Magnetisierungsstrom, der es spät E1 von 90 ° erzeugt, erzeugt. Im Schaltungsmodell würde IM daher durch die XM -Magnetisierungsreaktanz durch E1 gezeichnet.