Mit dem dBm-Watt-Konverter können Sie die in Milliwatt-Dezibel (dBm) ausgedrückte Leistung in tatsächliche Leistung in Watt umwandeln.
Diese Berechnung wird häufig in HF-Systemen, Telekommunikations- und Elektronikdesigns verwendet, um Signalleistungspegel zu vergleichen.
Verwendete Formel
Die Umrechnung zwischen dBm und Watt erfolgt nach folgender Formel:
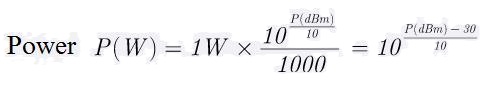
P(W) = 10 (P(dBm) / 10) / 1000
Dabei ist P(dBm) die Leistung in Milliwatt-Dezibel und P(W) die entsprechende Leistung in Watt.
Erklärung der Formel
Das dBm ist eine logarithmische Leistungseinheit relativ zu 1 Milliwatt.
Die Umkehrformel wandelt diesen logarithmischen Wert in eine lineare Potenz um.
Die Division durch 1000 ergibt die Leistung in Watt, denn 1 W = 1000 mW.
Verwenden
Diese Umwandlung wird verwendet, um die tatsächliche Leistung zu bestimmen, die von einem HF-Gerät gesendet oder empfangen wird.
wie einem Sender, Verstärker oder einer Antenne. Es ist unerlässlich beim Entwurf und der Messung von Funksignalen oder drahtlosen Netzwerken.
Berechnungsbeispiel
Nehmen Sie eine Leistung von P(dBm) = 30 dBm an .
Durch Anwendung der Formel:
P(W) = 10 (30 / 10) / 1000 = 10 3 / 1000 = 1 W
Der Wert von 30 dBm entspricht also 1 Watt Leistung.
Berechnungstipps
- Stellen Sie sicher, dass der Eingabewert in dBm und nicht in dBW ausgedrückt wird.
- Um dBW in Watt umzurechnen, verwenden Sie die Formel P(W) = 10 (P(dBW)) .
- Verwenden Sie immer eine ausreichende Genauigkeit, um Umrechnungsfehler bei niedrigen Leistungen zu vermeiden.
Warum diese Konvertierung verwenden?
Die dBm-Watt-Umwandlung verbindet die logarithmischen Einheiten, die bei der HF-Signalanalyse verwendet werden, mit den linearen Einheiten, die für die elektrische Leistung verwendet werden.
Es vereinfacht Vergleiche zwischen verschiedenen Komponenten eines Übertragungssystems.
Vorteile
- Ermöglicht die direkte Interpretation der Leistung in physikalischen Einheiten (Watt).
- Erleichtert den Entwurf und die Verifizierung von HF-Systemen.
- Verwendbar für jede Art von Leistungsmessung: Radio, Mikrowelle oder optische Signale.
Erwartetes Ergebnis: besseres Verständnis des Zusammenhangs zwischen logarithmischer Leistung und Wirkleistung.