Der Frequenz-Wellenlängen-Konverter berechnet die entsprechende Wellenlänge bei einer bestimmten Frequenz im Vakuum.
Dieses Tool ist für HF-Ingenieure, Antennendesigner und Forscher, die an der Ausbreitung elektromagnetischer Wellen arbeiten, unverzichtbar.
Verwendete Formel
Die Umrechnung beruht auf dem grundlegenden Zusammenhang zwischen Lichtgeschwindigkeit, Frequenz und Wellenlänge:
λ = c/f
Oder :
λ ist die Wellenlänge in Metern (m),
es ist die Lichtgeschwindigkeit im Vakuum (≈ 299 792 458 m/s),
f ist die Frequenz in Hertz (Hz).
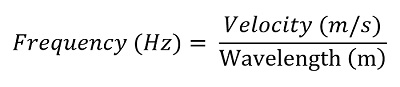
Erklärung der Formel
Diese Gleichung zeigt, dass die Wellenlänge umgekehrt proportional zur Frequenz ist.
Je höher die Frequenz, desto kürzer die Wellenlänge.
Dies ermöglicht es, das Verhalten von Signalen in verschiedenen Umgebungen zu verstehen, insbesondere in der drahtlosen Kommunikation, beim Radar oder in der Optik.
Verwenden
Diese Berechnung wird bei Funkübertragung, Antennendesign, Mikrowellen- und Glasfaseranwendungen verwendet.
Es hilft dabei, die physikalischen Abmessungen zu bestimmen, die für den Betrieb eines Geräts bei einer bestimmten Frequenz erforderlich sind.
Berechnungsbeispiel
Wenn die Frequenz f = 3 GHz ist:
λ = 299.792.458 / (3 × 10⁹) = 0,0999 m
Die entsprechende Wellenlänge beträgt daher etwa 0,1 m (10 cm).
Berechnungstipps
- Stellen Sie sicher, dass die eingegebene Frequenz positiv ist und korrekt ausgedrückt wird (Hz, kHz, MHz oder GHz).
- Für andere Medien als Vakuum verwenden Sie die entsprechende Ausbreitungsgeschwindigkeit (v = c / √εr).
- Hohe Frequenzwerte ergeben sehr kleine Wellenlängen, die in der Elektronik oder Optik nützlich sind.
Warum diese Konvertierung durchführen?
Durch die Umrechnung einer Frequenz in eine Wellenlänge können wir die mit dem Signal verbundene physikalische Größe verstehen.
Diese Informationen sind für den Entwurf von Antennen, die Berechnung von Resonanzen oder die Planung von Funkverbindungen unerlässlich.
Vorteile
- Ermöglicht die direkte Verknüpfung von Frequenz und physikalischer Dimension von Wellen.
- Nützlich für HF-, Mikrowellen-, optische und drahtlose Systeme.
- Erleichtert die Justierung von Antennen und Schwingkreisen.
Erwartetes Ergebnis: eine klare Übereinstimmung zwischen der Frequenz eines Signals und der zugehörigen Wellenlänge.