Äquivalente Induktionsmotorschaltung:
Äquivalente Induktionsmotorschaltung – Das Verhalten der Induktionsmaschine wurde im Hinblick auf das Grundphänomen des Feldes untersucht. Der Versuch hier konzentrierte sich absichtlich auf die Analogie des Induction -Engine -Transformators. Bestimmte bisher festgelegte Fakten sind nachstehend zusammengefasst:
1 und 1
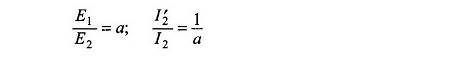
wobei E2 = Rotor des EMK -Urteils.
Zusätzlich fließt ich 2 in das positive Terminal der E1- und I2 -Flüsse aus dem positiven Terminal von E2. Darüber hinaus ist I2, wie der Stator zeigt, der Strom der Frequenz des Stators F und steht im Einklang mit der 2, der Komponente des vom Stators gezogenen Stroms, um den Rotor MMF F2 auszugleichen.
2. Wie in einem Transformator bleibt die IM -Magnetisierungsstromkomponente des Statorstroms hinter der EMF zurück, die durch den Stator E1 von 90 ° induziert wird.
3. Die Induktionsmotor ist nicht nur ein Transformator, der die Spannung und die Stromniveaus ändert. Es verhält sich tatsächlich als verallgemeinerter Transformator, in dem die Frequenz auch in den Verhältnis zum Schieben umgewandelt wird, so dass die vom Rotor induzierte EMF SE2 ist und die Reaktanz des Rotors SX2 ist.
Der Schaltungsäquivalent zur Induktionsmotor kann nun nach Phase wie in Abbildung 9.7 (a) gezeichnet werden, in der die Elemente der Serie (gruppiert) des Widerstands des Stators und der Lecksreaktanz in das Modell aufgenommen wurden.
Der Transformator, der die Stator- und Rotorschaltungen verbindet, ist ein idealer allgemeiner Transformator, bei dem die Spannung des Rotors des E2 -Stopps und der Strom des Rotors I2 über das Transformationsverhältnis A mit den Größen des Stators verbunden ist, während der Frequenzparameter im Schaltkreis des Rotors durch den Schleim ein mechanischer Parameter erscheint. Die mechanische Ausgangsleistung erscheint auf dem in der Abbildung angegebenen Baum.
Die Rotorschaltung kann durch einen zwei -stelligen Prozess, der die Rotorschaltung modifiziert, so an die Statorseite überwiesen werden, so dass das Kurvenverhältnis zum Einheit und dann eine Frequenztransformation durchführt, die sich aus einem Rotorschaltungskreis ergibt, der der Frequenz des Stators entspricht.
Durch Multiplizieren der Rotorspannung mit A und den Strom des Rotors mit 1 / A wird die Impedanz des Rotors für modifiziert
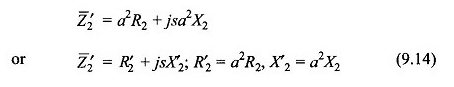
In dieser Transformation bleibt die Macht unveränderlich. Die Rotorkreis ist nach diesem Schritt in Abbildung 9.7 (b) gezogen. Dies reduziert den Rotor auf einen äquivalenten Rotor mit einem Einheits -Kurven -Verhältnis mit dem Stator.
Aus dem Rotorschaltungskreis entspricht Abbildung 9.7 (b)

Teilen Sie sowohl den Zähler als auch den Nenner durch s

Diese einfache Spitze bezieht sich auf den Rotorkreis an der Statorfrequenz. Die modifizierte Rotorschaltung ist jetzt in Abbildung 9.7 (c) gezeichnet, in der der Rotor- und Statorschaltkreis die gleiche Frequenz aufweist, der ideale Transformator ist jetzt ein stationärer Einheitsverhältnistransformator.
Es wird auch festgestellt, dass durch Überweisung des Rotorschalters auf die Statorfrequenz konstant wird (x’2) und der Widerstand variabel (r’2 / s). Die Transformation der Gleichung. (9.15b) ist keine invariante Leistung (Spannungsänderungen, während der Strom gleich bleibt).
Die in die Sekundarschule übertragene Leistung erklärt nun sowohl den Kupferverlust des Rotors als auch die mechanische Leistung (in elektrischer Form). Dies steht im Gegensatz zu Abbildung 9.7 (a), bei der die mechanische Leistung über einen Baum entfernt wird.
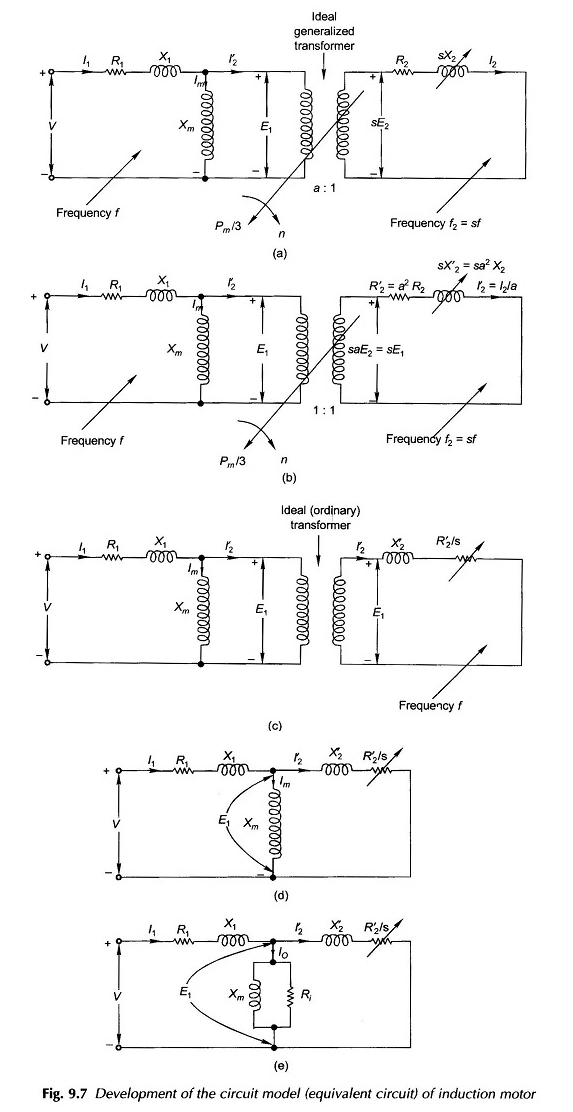
In der letzten Stufe der Entwicklung von äquivalenten Induktionsmotorschaltungen kann der ideale Einheitsverhältnistransformator (gewöhnlich) nun das Schaltungsmodell in Abbildung 9.7 (d) bereitgestellt werden.
Die Darstellung des Eisenverlusts im Stator kann heuristisch in das Schaltungsmodell von Abbildung 9.7 (d) eingeführt werden, indem ein Widerstands -RI parallel zu XM wie im Schaltungsmodell des Transformators platziert werden. Dieser Schaltkreis entspricht dem Induktionsmotor in Abbildung 9.7 (e).
Wenn R’2 von r’2 / s zur Darstellung des Kupferverlusts des Rotors als eigenständige Entität getrennt ist, kann das Schaltungsmodell wie in Abbildung 9.8 (a) gezeichnet werden, in dem der variable Widerstand R’2 (1 / s – 1) den mechanischen Ausgang in elektrischer Form darstellt. Alternativ das Schaltungsmodell von Abb.
9.8 (b) könnte verwendet werden (dies entspricht Abbildung 9.7 (d), in der der Widerstand gegen den Verlust von Eisen la weggelassen wird und dieser Verlust vom Brutto -mechanischen Ausgang subtrahiert wird (Leistung von R’2 (1 / s – 1)).
Dies entspricht bestimmten Näherungen, die im normalen Gleitbereich in einem Induktionsmotor völlig akzeptabel sind. Zusätzlich können die Parameter dieser Schaltung (die den RI-Wert nicht benötigen) durch zwei Nichtlasttests leicht erhalten werden.
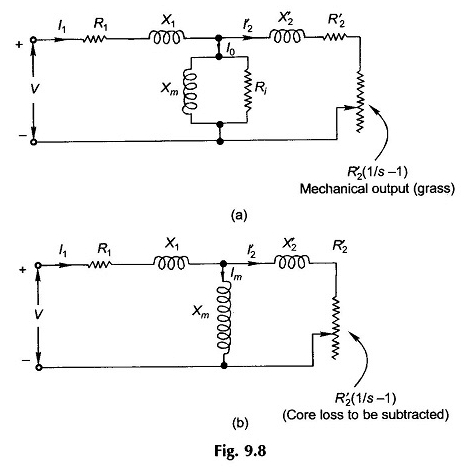
Das Schaltungsmodell in Abbildung 9.8 (b) wird für die meisten folgenden Diskussionen verwendet. Wir können hier feststellen, dass die in R’2 (1 / s – 1) gelöste Leistung den Grundverlust enthält, der subtrahiert werden muss, um die grobe mechanische Leistung zu erhalten.
Um eine klare mechanische Leistung zu erhalten, muss der Verlust von Wind und Reibung stärker abgezogen werden. Der Grundverlust und der Windverlust und der Reibungsverlust werden als Rotationsverlust gruppiert, da diese beiden Verluste beim Laufen des Motors auftreten.
Der Drehverlust in einem Induktionsmotor ist signifikant konstant zu einer konstanten angelegten Spannung und die Geschwindigkeit des Motors variiert nur sehr wenig von Volllast bei Volllast.
Hinweis: Mechanische Nettoleistung = Baumleistung