Modellierung der dynamischen Induktionsmotor:
Im Allgemeinen ist die mechanische Konstante für jede Maschine viel größer als die elektrische Zeitkonstante. Folglich kann die dynamische Modellierung der Induktionsmotor vereinfacht werden, indem der elektrische Übergang ohne Genauigkeit der Ergebnisse vernachlässigt wird.
Das Induktionsmotor -Schaltungsmodell ist für ein konstantes Gleiten vorhanden, würde aber auch ein langsam variierendes Gleiten anwenden, wie dies im Allgemeinen bei Beginn des Motors der Fall ist.
Abbildung 9.64 zeigt das typische Drehmoment -Gleitcharakteristik (Geschwindigkeit) der Modellierung der dynamischen Induktionsmotor und auch das Lastdrehmoment als Funktion des Gleitens (Geschwindigkeit).
Jeder Punkt auf der Eigenschaft (TL-S) repräsentiert das Drehmoment (Reibung), das von der Last und dem Motor erforderlich ist, wenn sie mit regelmäßiger Geschwindigkeit arbeiten. Der Motor würde nur dann beginnen, wenn t> tl eine regelmäßige Betriebsgeschwindigkeit von ω0 erreichen, die T = TL entspricht, dh zu sagen
Der Schnittpunkt p der beiden Drehmomentdrehzahlmerkmale. Es kann durch die Störmethode verifiziert werden, dass P ein stabiler Betriebspunkt für die Merkmal der angegebenen Ladegeschwindigkeit ist.
Wenn aus irgendeinem Grund die Geschwindigkeit größer als ω0, (t – tl) <0, verlauft die Maschinenlastkombination und kehrt zum Betriebspunkt zurück. Das Gegenteil tritt auf, wenn die Geschwindigkeit unter ω0 abnimmt.

Während der Beschleunigungsphase

wobei j = kombinierte Trägheit des Motors und der Last. JETZT

Daher ist Gl. (9.87) modifiziert zu

Integration
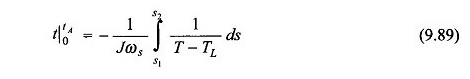
Da der Begriff 1 / (t – tl) nicht linear ist, Integration in die Gleichung. (9.89) muss grafisch (oder digital) wie in Abbildung 9.65 für den Fall ausgeführt werden, wenn S1 = 1 und S2 = S0.
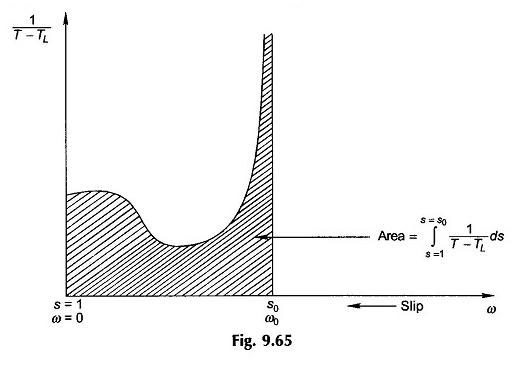
Da 1 / (tl) zu S0 wird, wird die praktische Integration je nach gewünschter Präzision nur bis zu 90 oder 95% S0 durchgeführt.
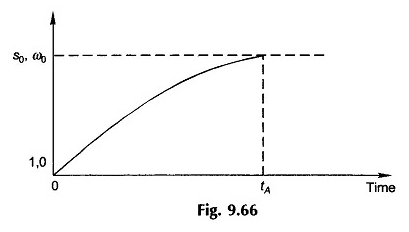
Abbildung 9.66 zeigt, wie sich die Schiebung (Geschwindigkeit) im Laufe der Zeit während der Beschleunigungszeit mit dem regulären Wert von S0 (ω0) in der Zeit und Beschleunigungszeit variiert. Aufgrund der Nichtlinearität von (t – tl) in Abhängigkeit von der Verschiebung ist die Gleitkurve (Geschwindigkeit) in Abbildung 9.66 nicht exponentiell.
Beginnend ohne Last (TL = 0):
In diesem speziellen Fall wird angenommen, dass die Maschine und das Drehmoment der Ladung von Reibung TL = 0.
Unter der Annahme, dass Statorverluste vernachlässigbar sind (d. H. R1 = 0), wurde das von der Gleichung erhaltene Motordrehmoment. (9.22) ist
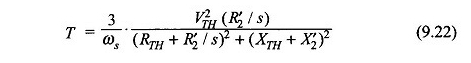
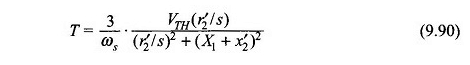
Auch der Gleichung. (9.24)
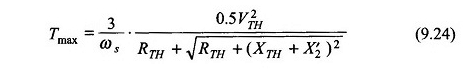

zu einer Verschiebung in (Gleichung (9.23))
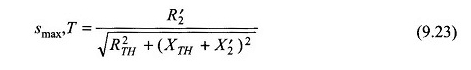

Aus den Gleichungen (9.90) und (9.91),,
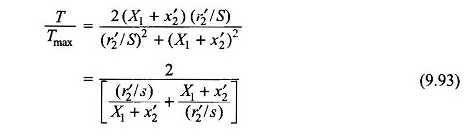
Ersetzen der Gleichung. (9.92) in (9.93)
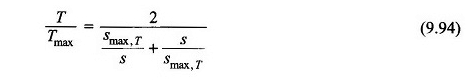
Da angenommen wird, dass TL Null ist, ist das Motordrehmoment selbst das beschleunigte Drehmoment,
Das heißt
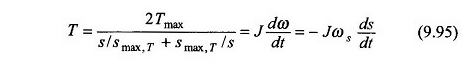
TI zum Umschalten von Shift S1 nach S2 wird während der Integration der Gleichung erhalten. (9.95) as
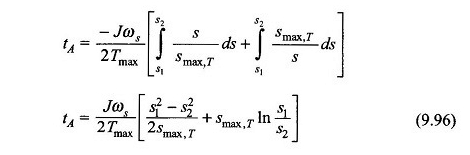
Die Beschleunigungszeit, sodass die Maschine den regulären Start von Start -up erreicht, kann aus der Gleichung berechnet werden. (9.96) mit S1 = 1 und S2 = S, das heißt

Optimal SMAX, T für die minimale Beschleunigungszeit:
Um den optimalen Wert von SMAX zu ermitteln, t dynamische Einführungsmotormodellierung, um eine minimale Beschleunigungszeit zu haben, um S2 von S1, Gl. (9.96) müssen von SMAX, T und Null unterschieden werden. Es gibt

Für eine minimale Beschleunigungszeit, damit die Maschine von Anfang an einen Schlupf erreicht, wird der optimale Wert von SMAX durch die Gleichung angegeben. (9,98) mit S1 = 1 und S2 = S. Also also

Und

Darüber hinaus können wir den optimalen Wert des Rotorwiderstandes berechnen, um die Maschine auf S2 zu beschleunigen, Gl. (9.98) wird in Gl. (9.92) Geben Sie
