Analyse der Übergangsinduktionsmotor:
Die Nützlichkeit der Analyse der Übergangsbetriebsbedingungen eines Lesers, zum Beispiel Start, Bremsen, Laständerung, Geschwindigkeitsänderung usw., wird bereits erläutert.
Eine strenge Analyse des Übergangsbetriebs eines Induktionsmotorantriebs kann nur durch das DQ -Achsenmodell durchgeführt werden, das lange Berechnungen umfasst. Eine einfache analytische Methode mit zufriedenstellender Präzision für die meisten Anwendungen wird unter Verwendung dauerhafter Paarbeziehungen erhalten.
Eine solche Analyse basiert auf der Hypothese, dass die elektrischen Zeitkonstanten vernachlässigt werden können, da sie im Vergleich zur mechanischen Zeitkonstante sehr gering sind. Daher können wir die folgende Gleichung für die Übergangsanalyse des Induktionsmotortrainings schreiben:
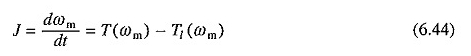
Die Gleichung (6.44) kann grafisch bewertet werden, um die ωm vs T -Kurve und die Energieverluste im Motor- und externen Rotorwiderstand unter Verwendung der bereits erklärten Methode zu erhalten.
Dieser Ansatz ist allgemein und kann für jede transiente Analyse des Induktionsimers verwendet werden, solange die Geschwindigkeitsgeschwindigkeitskurven in der permanenten Motordrehzahl [t (ω)] und die Last [T1 (ωm)] bekannt sind. Ungefähr analytische Methoden werden nachstehend dargestellt.
Start und Stecker:
Um den Betrieb der Maschine zu starten und zu verbinden, wird das Drehmoment durch die Gleichung angegeben. (6.15). Ersetzen der Gleichung. (6.15) in (6.44) Ausbeuten
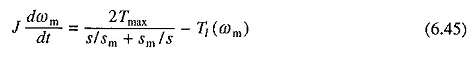
In einigen Fällen die Gleichung. (6.45) befindet sich in integrierbarer Form und kann daher analytisch aufgelöst werden. Es ist nützlich, Transienten zum Starten und Anschluss von Vorgängen beim Betrieb ohne Last zu untersuchen. So der Gleichung. (6.45) für keinen Ladevorgang

Differenzierung der Gleichung. (6.3) gibt

Ersetzen der Gleichung. (6.47) in (6.46) und die Begriffe neu organisieren

τm ist die mechanische Zeitkonstante des Motors. Es ist definiert als die Zeit, die der Motor benötigt, um die Synchrongeschwindigkeit des Stopps unter einem konstanten beschleunigenden Drehmoment zu erreichen, das dem maximalen Drehmoment des Motors entspricht.
Der Gleichung. (6.48) ist die Zeit, die zum Starten eines Induktionsmotors für jede Last erforderlich ist
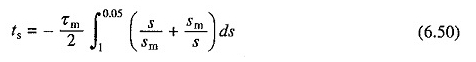
Während der Operation bei No Last wird der Gleichgewichtszustand erreicht, wenn s = 0. Während der Start -up ändert sich die Verschiebung von 1 auf 0. Wenn (6,50) jedoch für s = 1 bis s = 0 integriert ist, wird für die Startzeit ein unendlicher Wert erhalten.
Wie erläutert, gelten die Transientarien, wenn die endgültige Geschwindigkeit die Gleichgewichtsgeschwindigkeit im Gleichgewichtszustand ist, als höher, wenn der Geschwindigkeitsbereich von 95% abgedeckt ist. Daher in Gl. (6.50) Die Integration erfolgt von S = 1 bis S = 0,05. Auflösung (6.50) gibt

Somit hängt die Startzeit von SM ab. Die Startzeit hat einen Mindestwert von 1,22 τm bis SM = 0,4. Der Gleichung. (6.12) Wenn RS vernachlässigbar ist, ist der Rotorwiderstand, der zum Starten des Motors erforderlich ist, zumindest

Der Gleichung. (6.48) kann die Zeit, die erforderlich ist, um durch Verbindung zu stehen, wenn er anfänglich mit einer synchronen Geschwindigkeit läuft, ausgedrückt werden als
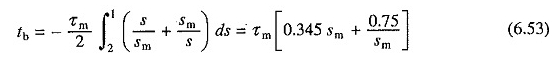
Die Ausfallzeit ist wieder eine Funktion von SM. Es hat einen Mindestwert von 1,027 τm zu SM = 1,47. Der entsprechende Wert des Widerstands gegen den Rotor ist
![]()
Ebenso aus der Gleichung. (6.48) Die für die Umkehrung der Geschwindigkeit erforderliche Zeit durch Anschließen während der Ausführung bei einer beladenen Ladung ist gegeben von
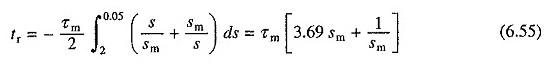
Die Mindestzeit für die Umkehrung beträgt daher 2,88 τm und der entsprechende Wert von SM 0,52. Der für die Geschwindigkeitsumkehr erforderliche Rotorwiderstand durch Anschließen der Mindestzeit ist
![]()
Berechnung von Energieverlusten:
Lassen Sie uns als nächstes die Ausdrücke für den Energieverlust bei Motorwicklungen zum Starten und Anschluss von Betriebsvorgängen planen. Der Verlust der Rotorwicklung für den Start -up kann geschrieben werden

Gleichungen ersetzen. (6.5) und (6.11) gibt an

Da arbeitet die Maschine unter jeder Last

Ersetzen der Gleichung. (6.47)
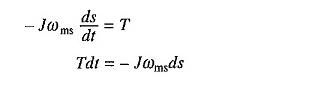
Oder
Ersatz in (6.58) gibt
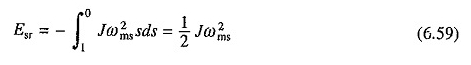
Es ist interessant festzustellen, dass der Energieverlust der Rotorwicklung der kinetischen Energie entspricht, die nach Abschluss des Startvorgangs in mobilen Teilen gespeichert ist, und unabhängig von der Abfahrtszeit oder dem Rotorwiderstand.
Wenn jedoch ein externer Widerstand im Rotorkreis angeschlossen ist, wird nur ein Teil dieses Verlustes verwendet, um den Motor zu erwärmen. Energieverlust bei der Statorwicklung, vernachlässigt der Magnetisierungsstrom

Daher beträgt der Gesamtwicklungsverlust während des Starts unter jeder Last

Machen Sie die Miladie, der Verlust der Drehung des Rotors beim Anhalten durch Anschließen ohne Last kann geschrieben werden

Die Gleichung (6.59) legt nahe, dass der Verlust der Rotorwicklung reduziert werden kann, wenn sie mit Methoden auf der Grundlage der Variation der synchronen Geschwindigkeit begann. Betrachten Sie beispielsweise einen Motor mit einer Anordnung, um die Postnummer zu verdoppeln.
Lassen Sie es mit einer höheren Polnummer beginnen, für die die Synchrongeschwindigkeit ωms / 2. beträgt. Dann ist (6.59) der Kupferverlust des Rotors für die Geschwindigkeitsänderung von 0 auf ωms / 2 Jω2ms / 8. Jetzt wird die Polzahl gesenkt. Folglich ist der Kupferverlust des Rotors für den Geschwindigkeitsbereich ωms / 2 in ωms
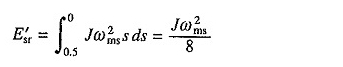
Somit beträgt die Gesamtwicklung des Rotors Jω2ms / 4, was der halbe Kupferverlust ist, wenn es nicht vorkommt, die Pole -Zahl zu verdoppeln.