Il calcolatore della frequenza di risonanza del circuito LC consente di determinare la frequenza alla quale un circuito composto da un’induttanza (L) e una capacità (C) entra in risonanza.
Questa frequenza è essenziale per progettare filtri, oscillatori e circuiti RF e per garantire che il circuito funzioni correttamente alla frequenza desiderata.
Formula utilizzata
f = 1 / (2 × π × √(L × C))
O :
L = induttanza del circuito (H, mH, µH o nH)
C = capacità del circuito (F, µF, nF o pF)
f = frequenza di risonanza (Hz o GHz)
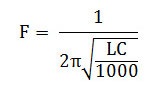
Spiegazione
La frequenza di risonanza è il punto in cui la reattanza induttiva e la reattanza capacitiva si annullano a vicenda.
A questa frequenza, il circuito LC può oscillare liberamente con la massima ampiezza, il che è fondamentale per i filtri passa banda, i circuiti oscillatori e i dispositivi RF.
Utilizzo
Questo strumento viene utilizzato da ingegneri RF, tecnici elettronici e studenti per:
- Calcolare l’esatta frequenza di risonanza per un dato circuito.
- Ottimizzare la progettazione di filtri e oscillatori.
- Evitare offset di frequenza indesiderati nei circuiti RF.
Esempio di calcolo
Per un circuito con L = 50 nH e C = 10 pF :
f = 1 / (2 × π × √(50×10 -9 × 10×10 -12 )) ≈ 22,52 GHz
Suggerimenti per il calcolo
- Verificare che le unità di induttanza e capacità siano coerenti.
- Per i circuiti ad alta frequenza utilizzare valori molto precisi per L e C in modo da non spostare la frequenza di risonanza.
- Sperimenta valori diversi per osservare l’effetto sulla frequenza di risonanza.
Perché questo calcolo è importante
Determinare correttamente la frequenza di risonanza garantisce che il circuito LC funzioni come previsto e che il trasferimento di energia sia ottimale.
È un elemento chiave nella progettazione di circuiti RF e nella calibrazione di sistemi elettronici.
Vantaggi
- Permette di anticipare le prestazioni di un circuito LC prima della sua realizzazione.
- Aiuta a progettare oscillatori e filtri accurati.
- Applicabile a tutti i tipi di circuiti RF ed elettronici che utilizzano componenti L e C.
Risultato atteso: la frequenza di risonanza del circuito LC, espressa in GHz, che indica dove il circuito oscillerà in modo ottimale.