Circuito equivalente armonico del motore a induzione:
Se alimentato da un inverter o da un cicoconettivo, il controllo del terminale motorio è non-sinusoidale ma ha una simmetria a mezza onda. Una forma d’onda non sinusoidale può essere risolta in componenti fondamentali e armonici usando l’analisi di Fourier.
A causa della simmetria a mezza onda, saranno presenti solo strane armoniche. Il circuito equivalente armonico del motore di induzione può essere diviso in sequenza positiva, sequenza negativa e sequenza zero.
Le armoniche, che hanno la stessa sequenza di fasi di quella fondamentale, sono chiamate armoniche della sequenza positiva. Il circuito equivalente armonico del motore di induzione con una sequenza di fasi contrarie a fondamentali è chiamato armonica della sequenza negativa. Le armoniche, che hanno tutte le tre tensioni in fase in fase, sono chiamate armoniche di sequenza zero.
Considera i componenti di tensione di fase fondamentali van = v1 sin ωt, vbn = v1 sin (ωt -2π / 3) e vcn = v1 sin (ωt – 4π / 3) con la sequenza di fase ABC. Le corrispondenti tensioni di fase armonica sono le corrispondenti

Le equazioni di cui sopra mostrano che la settima armonica ha la sequenza della fase ABC, che è la stessa di quella fondamentale. È quindi un’armonica di sequenza positiva. La quinta armonica ha una sequenza di fasi ACB, quindi è un’armonica della sequenza negativa.
Possiamo dimostrare che le tensioni armoniche e le correnti dell’ordine M = 6K + 1 (dove K è un numero intero) sono di sequenza positiva e le tensioni armoniche dell’ordine M = 6K – 1 sono sequenze negative.
Allo stesso modo, si può dimostrare che le armoniche dell’ordine M = 3K sono sequenze zero. Un’armonica di sequenza positiva produrrà un campo rotante, che si muove nella stessa direzione del fondamentale a una velocità m volte quello del campo fondamentale.
Il campo rotante simile produce con una sequenza negativa L’armonica M si sposterà nella direzione opposta alla velocità fondamentale alla sua velocità. I componenti di sequenza zero non producono un campo rotante.
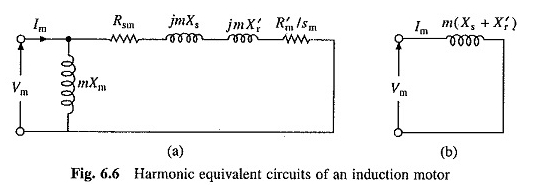
Per la componente fondamentale, saranno applicabili i circuiti equivalenti della Figura 6.1. Per qualsiasi MTH armonico, il circuito equivalente sarà come mostrato nella Figura 6.6 (a). Ogni reattanza è stata aumentata di un fattore M. A causa degli effetti della pelle, anche i resistori saranno aumentati più volte. Slipping SM per l’armonica MTH è dato da

Il segno negativo è applicabile alle armoniche che producono campi rotanti in avanti e al segno positivo per coloro che producono campi rotanti all’indietro. Poiché SM è vicino all’unità, la resistenza ((R′RN / SM)) ha un valore piccolo.
Poiché le reattanze sono molto grandi rispetto ai resistori, il circuito equivalente della Figura 6.6 (a) può essere sostituito dal circuito semplificato nella Figura 6.6 (b).
Quando viene alimentato da un convertitore a semiconduttore, si può dimostrare che la coppia netta prodotta dalle armoniche è vicina allo zero. Data questa coppia del motore, può essere valutata da circuiti equivalenti nella Figura 6.1 (b), usando l’equazione. (6.10), dove V è la componente fondamentale della tensione di alimentazione.
La componente fondamentale della corrente del rotore è ottenuta dall’equazione. (6.4) e la corrente armonica / n.

dove xs + x′r.
Generalmente, l’offerta avrà strane armoniche. Quando lo statore è armonico Tripplen collegato alla stella (la terza armonica e il suo multiplo) non scorrerà. La corrente del motore IRMS RMS sarà quindi

Quando il motore è collegato al delta, le armoniche di Tripplen circolano nel delta, ma non scorreranno nella sorgente. La corrente di origine può quindi essere ottenuta moltiplicando la risonanza magnetica data dall’equazione. (6.24) di √3. La corrente di fase del motore RMS sarà ottenuta da
![]()
Per una determinata coppia e potenza di potenza, la corrente RMS che scorre nel motore ha un valore più elevato. Inoltre, a causa dell’effetto della pelle, la resistenza ai rotori armonici ha un valore più elevato. Di conseguenza, la presenza di armoniche aumenta considerevolmente la perdita di rame.
Anche le perdite di base sono aumentate dalle armoniche. A causa dell’aumento delle perdite, il motore deve essere deluso nel senso che la potenza che può essere ottenuta dalla macchina per lo stesso aumento della temperatura deve essere più piccola. L’efficienza è inoltre ridotta a causa dell’aumento delle perdite.
Un altro effetto importante del cibo non sinusoidale è la produzione di coppie pulsanti a causa dell’interazione tra il campo rotante prodotto da una corrente armonica e il rotore di un’altra armonica. Le armoniche 5, 7, 11 e 13 contribuiscono ai principali impulsi di coppia.
La quinta armonica produce un campo rotante all’indietro mentre la settima armonica produce un campo rotante in avanti. Di conseguenza, la velocità relativa tra il campo prodotto dalle armoniche fondamentali e il 5 ° e il 7 ° è sei volte la velocità di fondamentale.
Di conseguenza, gli impulsi di coppia prodotti a causa dell’interazione delle correnti armoniche del 5 ° e 7 ° e il campo rotante fondamentale hanno una frequenza sei volte il fondamentale.
Si può anche dimostrare che le armoniche 11 e 13 producono impulsi di coppia la cui frequenza è 12 volte il fondamentale. Quando la frequenza della fornitura del motore non è molto bassa, la frequenza degli impulsi di coppia è abbastanza grande da essere filtrata dall’inerzia del motore.
Di conseguenza, le pulsazioni di coppia non hanno alcun effetto significativo sulla velocità del motore, sebbene aumentino il rumore e riducano la durata del motore a causa delle vibrazioni. Tuttavia, quando la frequenza della fornitura del motore è bassa, questi impulsi di coppia causano impulsi di velocità. Il motore non si muove delicatamente ma ha un movimento a scatti.