Circuito del motor
Circuito del motore a induzione equivalente:
Circuito del motore a induzione equivalente – Il comportamento della macchina a induzione è stato studiato in termini di fenomeno di base sul campo. Il tentativo qui si è concentrato deliberatamente sull’analogia del trasformatore del motore a induzione. Alcuni fatti stabiliti finora sono riassunti di seguito:
1 e 1
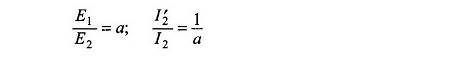
dove e2 = rotore del giudizio EMF.
Inoltre, I’2 scorre nel terminale positivo di E1 e I2 fluisce dal terminale positivo di E2. Inoltre, I2, come mostra lo statore è la corrente della frequenza dello statore F ed è in linea con il 2, il componente della corrente disegnata dallo statore per bilanciare il rotore MMF F2.
2. Come in un trasformatore, la componente di corrente magnetizzante IM della corrente dello statore è in ritardo dietro l’EMF indotta dallo statore E1 di 90 °.
3. Il motore a induzione non è solo un trasformatore che cambia la tensione e i livelli di corrente. In realtà si comporta come un trasformatore generalizzato in cui anche la frequenza viene trasformata in proporzione per scivolare in modo che l’EMF induce dal rotore è SE2 e la reattanza del rotore è SX2.
Il circuito equivalente al motore a induzione può ora essere disegnato per fase come nella Figura 9.7 (a) in cui gli elementi della serie (raggruppati) della resistenza dello statore e la reattanza di perdite sono stati inclusi nel modello.
Il trasformatore che collega lo statore e i circuiti del rotore è un trasformatore generale ideale in cui la tensione del rotore dell’arresto E2 e la corrente del rotore I2 sono collegate alle quantità dello statore attraverso il rapporto di trasformazione A, mentre il parametro di frequenza appare nel circuito del rotore attraverso la Slissment S, un parametro meccanico. La potenza di uscita meccanica appare sull’albero indicato nella figura.
Il circuito del rotore può essere indirizzato al lato dello statore da un processo a due fasi che modifica il circuito del rotore in modo che il rapporto di svolta diventi l’unità e quindi esegue una trasformazione di frequenza, che deriva da un circuito del rotore equivalente alla frequenza dello statore.
Moltiplicando la tensione del rotore per a e la corrente del rotore per 1 / a, l’impedenza del rotore viene modificata per
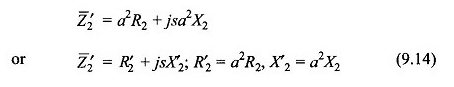
In questa trasformazione, il potere rimane invariante. Il circuito del rotore, dopo aver effettuato questo passaggio, viene disegnato nella Figura 9.7 (b). Ciò riduce il rotore a un rotore equivalente con un rapporto di svolta unitario con lo statore.
Dal circuito del rotore equivalente alla Figura 9.7 (b)

Dividi sia il numeratore che il denominatore di s

Questa semplice punta si riferisce al circuito del rotore alla frequenza dello statore. Il circuito del rotore modificato è ora disegnato nella Figura 9.7 (c) in cui il circuito del rotore e dello statore ha la stessa frequenza, il trasformatore ideale è ora un trasformatore di rapporto unitario stazionario.
Si noti inoltre che facendo riferimento al circuito del rotore alla frequenza dello statore, la reattanza diventa costante (X’2) e la resistenza diventa variabile (R’2 / s). La trasformazione dell’equazione. (9.15b) non è la potenza invariante (cambi di tensione mentre la corrente rimane la stessa).
La potenza trasferita alla scuola secondaria ora spiega sia la perdita di rame del rotore che la potenza meccanica (in forma elettrica). Ciò contrasta con la Figura 9.7 (a) in cui la potenza meccanica viene rimossa tramite un albero.
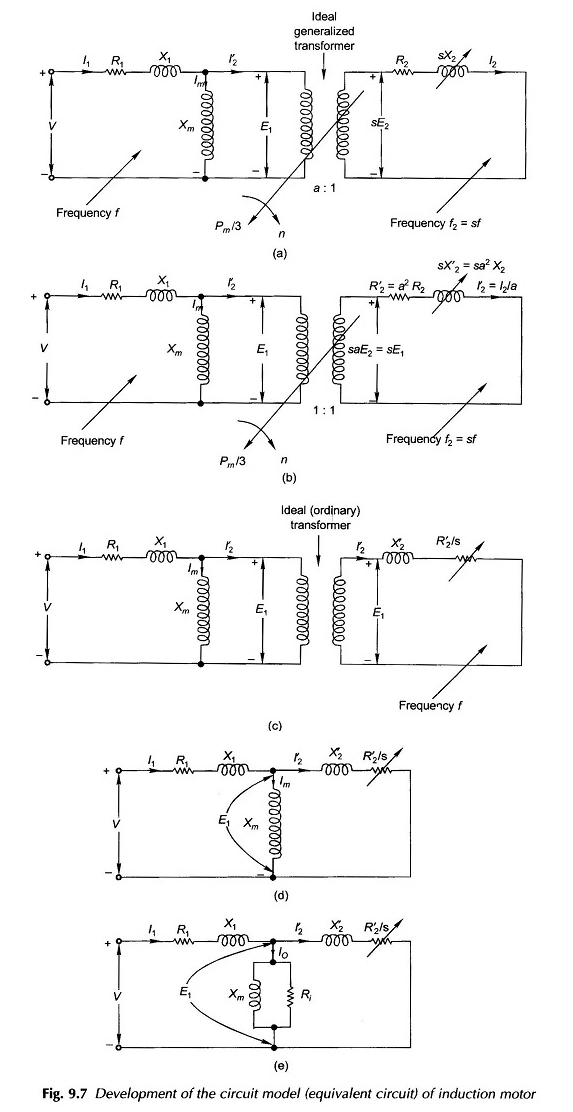
Nell’ultima fase dello sviluppo di circuiti motori a induzione equivalenti, il trasformatore del rapporto unitario ideale (ordinario) può ora essere fornito con il modello di circuito nella Figura 9.7 (d).
La rappresentazione della perdita di ferro nello statore può essere introdotta euristicamente nel modello del circuito della Figura 9.7 (d) posizionando una resistenza RI parallela con XM come nel modello del circuito del trasformatore. Questo circuito equivalente al motore a induzione è progettato nella Figura 9.7 (e).
Se R’2, è separato da R’2 / s per rappresentare la perdita di rame del rotore come entità distinta, il modello di circuito può essere disegnato come nella Figura 9.8 (a) in cui la resistenza variabile R’2 (1 / S – 1) rappresenta l’output meccanico in forma elettrica. In alternativa, il modello di circuito di Fig.
È possibile utilizzare 9.8 (b) (ciò corrisponde alla Figura 9.7 (d) in cui viene omessa la resistenza alla perdita di ferro LA e questa perdita verrebbe sottratta dall’uscita meccanica lorda (energia assorbita da R’2 (1 / S – 1)).
Ciò equivale a alcune approssimazioni che sono completamente accettabili nel normale intervallo di scorrimento in un motore a induzione. Inoltre, i parametri di questo circuito (che non richiedono il valore RI) possono essere facilmente ottenuti da due test di non carico.
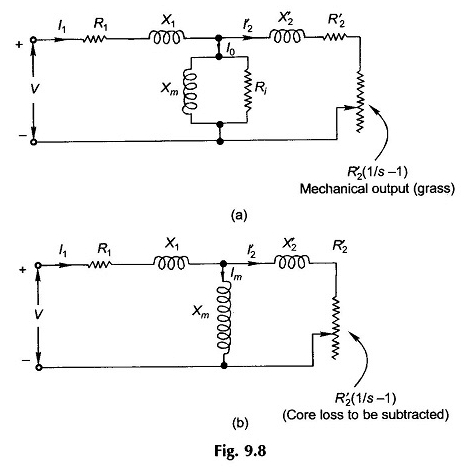
Il modello di circuito nella Figura 9.8 (b) verrebbe utilizzato per la maggior parte della discussione seguente. Possiamo notare qui che la potenza dissipata in R’2 (1 / s – 1) include la perdita di base, che deve essere sottratta per ottenere la potenza meccanica lorda.
Per ottenere una chiara potenza meccanica, la perdita di vento e attrito deve essere più sottratta. La perdita di base e la perdita del vento e la perdita di attrito sono raggruppate come perdita di rotazione perché queste due perdite si verificano quando il motore è in esecuzione.
La perdita di rotazione in un motore a induzione è significativamente costante a una tensione applicata costante e la velocità del motore varia molto poco da pieno carico a pieno carico.
Nota: potenza meccanica netta = potenza dell’albero