Modellazione del motore a induzione dinamica:
In generale, la costante meccanica per qualsiasi macchina è molto più grande della costante di tempo elettrico. Di conseguenza, la modellazione dinamica del motore a induzione può essere semplificata trascurando la transizione elettrica senza alcuna perdita di precisione dei risultati.
Il modello del circuito del motore a induzione è per uno scorrimento costante, ma si applicherebbe anche per uno scorrimento che varia lentamente, come generalmente accade all’inizio del motore.
La Figura 9.64 mostra la tipica caratteristica di scorrimento della coppia (velocità) della modellazione dinamica del motore a induzione e anche la coppia di carico in funzione dello scorrimento (velocità).
Ogni punto sulla caratteristica (TL-S) rappresenta la coppia (attrito) richiesta dal carico e dal motore quando operano a velocità regolare. Il motore si avvia solo se t> tl e raggiungere una velocità operativa regolare di ω0 che corrisponde a t = tl, vale a dire
Il punto di intersezione P delle due caratteristiche di velocità di coppia. Può essere verificato con il metodo di disturbo che P è un punto operativo stabile per la caratteristica della velocità di ricarica indicata.
Se per qualsiasi motivo, la velocità diventa maggiore di ω0, (t – tl) <0, la combinazione di carico della macchina si rallegra e ritorna al punto operativo. Il contrario si verifica se la velocità diminuisce al di sotto di ω0.

Durante il periodo di accelerazione

dove j = inerzia combinata del motore e del carico. ORA

Pertanto, Eq. (9.87) modificato a

Integrazione
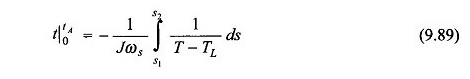
Poiché il termine 1 / (t – tl) non è lineare, l’integrazione nell’equazione. (9.89) deve essere eseguito graficamente (o digitalmente) come mostrato nella Figura 9.65 per il caso quando S1 = 1 e S2 = S0.
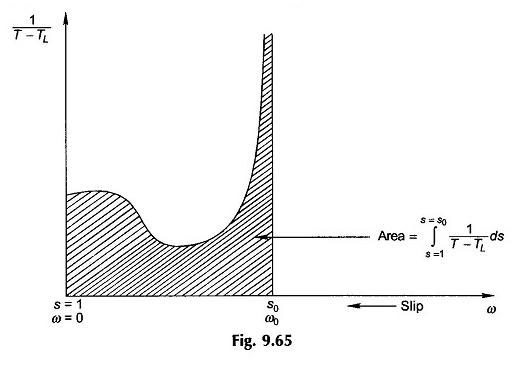
Poiché 1 / (TL) diventa da ∞ a S0, l’integrazione pratica viene effettuata solo fino al 90 o al 95% S0 a seconda della precisione desiderata.
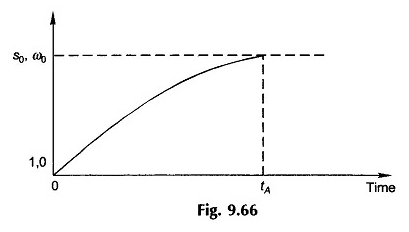
La Figura 9.66 mostra come la scorrimento (velocità) varia nel tempo durante il periodo di accelerazione raggiungendo il valore normale di S0 (ω0) nel tempo, tempo di accelerazione. A causa della non linearità di (t – tl) in funzione dello spostamento, la curva scorrevole (velocità) nella Figura 9.66 non è esponenziale.
A partire da carico (TL = 0):
In questo caso particolare, si presume che la macchina e la coppia di attrito di ricarica tl = 0.
Supponendo che le perdite dello statore siano trascurabili (ovvero R1 = 0), la coppia del motore ottenuta dall’equazione. (9.22) è
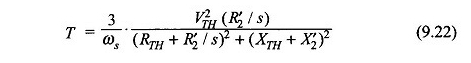
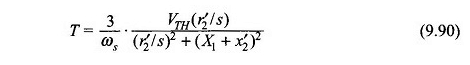
Anche dell’equazione. (9.24)
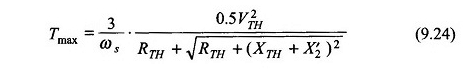

a uno spostamento in (eq. (9.23))
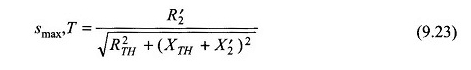

Dalle equazioni (9.90) e (9.91),
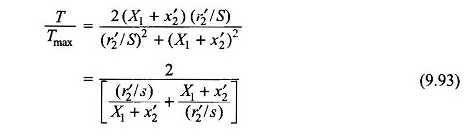
Sostituendo l’equazione. (9.92) in (9.93)
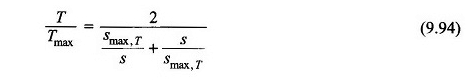
Poiché si presume che TL sia zero, la coppia del motore stesso è la coppia accelerata,
Questo per dire
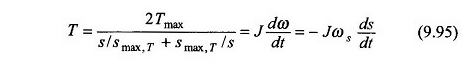
TI per passare da Shift S1 a S2 si ottiene durante l’integrazione dell’equazione. (9.95) AS
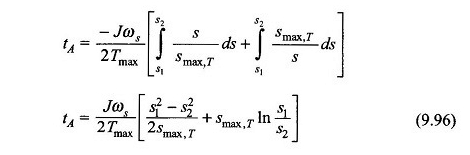
Il tempo di accelerazione in modo che la macchina raggiunga il normale inizio di avvio -up può essere calcolato dall’equazione. (9.96) con S1 = 1 e S2 = S, vale a dire

Smax ottimale, T per il tempo di accelerazione minima:
Per trovare il valore ottimale di Smax, T per la modellazione del motore di induzione dinamico per avere un tempo minimo di accelerazione per raggiungere S2 da S1, Eq. (9.96) deve essere differenziato da Smax, T e assimilato a zero. Dà

Per un tempo di accelerazione minimo affinché la macchina raggiunga qualsiasi slittamento dall’inizio, il valore ottimale di Smax, T è dato dall’equazione. (9.98) con S1 = 1 e S2 = S. SO

E

Inoltre, per consentirci di calcolare il valore ottimale della resistenza del rotore per accelerare la macchina per scorrere S2 da S1, Eq. (9.98) è sostituito in Eq. (9.92) dare
