Motori a induzione monofase
Motore a induzione monofase:
Un motore a induzione a fase singola include un avvolgimento distribuito a fase singola sullo statore e il normale rotore scoiattolo, come schematicamente illustrato nella Figura 10.1 in cui per comodità, l’avvolgimento dello statore è illustrato in forma concentrata.

Esistono due metodi importanti per analizzare questo motore, vale a dire
- Teoria del campo trasversale e
- Teoria dei campi rotanti.
Poiché quest’ultimo è più simile alla teoria della macchina a induzione a tre fasi avanzata in precedenza, verrà adottata qui.
Campo pulsante come due campi rotanti:
La Figura 10.1 fornisce lo schema schematico di un motore a induzione monofase con avvolgimento dello statore e un rotore di gabbia scoiattolo. L’avvolgimento è distribuito nello spazio in modo che lo spazio fondamentale di MMF sia la componente più dominante della distribuzione MMF reale.
Le armoniche spaziali di MMF, come nel caso di un motore di induzione in tre fasi, sarebbero quindi ignorate. Quando l’avvolgimento trasporta una corrente sinusoidale, produce un MMF distribuito nello spazio sinusoidalmente il cui valore di picco impulso nel tempo. Come mostra l’asse dell’avvolgimento, il mmf ad angolo θ è
![]()
dove θ è l’angolo misurato dall’asse di avvolgimento. ORA
![]()
in modo che l’MMF abbia sia una distribuzione dello spazio che il tempo espresso
![]()
Questa equazione può essere manipolata trigonometrica nella forma
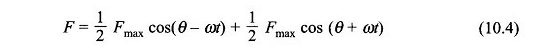
L’equazione (10.4) ci dice che un campo a fase singola pulsata può essere considerato come una sovrapposizione di due campi rotanti che funzionano a una velocità sincrona (ω = 2πf eletto. Rad / s) in direzioni opposte:

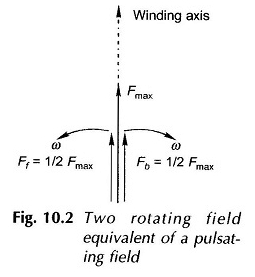
Questi due campi hanno un’ampiezza uguale a (1/2) FMAX in cui fmax è il valore massimo del pulsatorio MMF lungo l’asse dell’avvolgimento. La divisione di un singolo campo pulsato in due campi rotanti in esecuzione in direzioni opposte è illustrata nella Figura 10.2.
Questa figura mostra la posizione dei campi rotanti alla volta in cui l’MMF lungo l’asse di avvolgimento è + fmax.
Scorritura del rotore rispetto a due campi rotanti:

Per il caso unico illustrato nella Figura 10.1, la Figura 10.3 mostra i campi rotanti in avanti e indietro con il rotore che funziona a velocità n nella direzione del campo anteriore. Lo spostamento del rotore rispetto al campo rotante in avanti FF è quindi

Mentre il rotore scorre rispetto al campo di svolta FB

Pertanto, le diapositive del rotore rispetto ai due campi rotanti sono diversi e sono dati dalle equazioni (10,5a) e (10,5b).
Caratteristica della velocità del motore del motore a induzione monofase:
Trattamento qualitativo in uno stato di rotore stazionario (n = 0, vale a dire s = 1), i due campi rotanti scivolano davanti al rotore con lo stesso turno, s = 1, (vedi Eqs (10.5a) e (10.5b)) inducono correnti uguali nel rotore dello scoiattolo.
I due campi rotanti hanno la stessa resistenza e producono coppie uguali e opposte, che porta a una coppia di avvio netta di valore zero. Il singolo motore a induzione monofase singolo a vuoto è quindi un avvio non proper.
Inoltre, i due campi rotanti inducono un EMF risultante nello statore che bilancia la tensione applicata assumendo una bassa impedenza di perdite dell’avvolgimento dello statore.
Se, tuttavia, il rotore è progettato per funzionare a velocità n nella direzione del campo anteriore, i due turni sono ora s e (2 – s).
Per il normale funzionamento (2 – s) ≫ s e, quindi, le correnti del rotore indotte dallo sfondo sono molto più alte di quando sono fermate e hanno un fattore di potenza inferiore.
Il corrispondente MMF del rotore avversario, in presenza dell’impedenza dello statore, porta a una riduzione considerevolmente dal campo alla parte posteriore. D’altra parte, il campo rotante verso il basso spostamento induce correnti più piccole di un fattore di potenza più elevato nel rotore rispetto a quando interrotto.
Questo porta a un grande miglioramento dell’onda di flusso anteriore.
Questa riduzione dal campo alla parte posteriore e il rafforzamento del campo anteriore dipende dallo spostamento e la differenza aumenta quando il slisement S (rispetto al campo anteriore) si è ridotto o la velocità del rotore nella direzione anteriore diventa vicino alla velocità sincrona.
In effetti, vicino alla velocità sincrona, il campo anteriore può essere il campo più volte. Di conseguenza, c’è una coppia di net. I due campi devono sempre indurre l’avvolgimento EMF dello statore per bilanciare la tensione applicata.
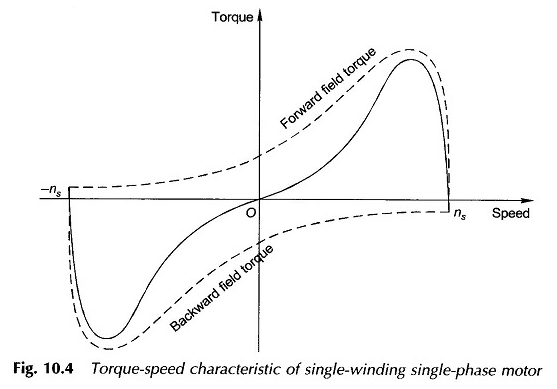
La caratteristica completa della velocità di coppia come somma delle due caratteristiche di velocità di coppia (anteriore e posteriore) è disegnata nella Figura 10.4.
Il risultato dell’indebolimento di un campo e del rinforzo simultaneo dell’altro porta a una caratteristica della velocità di coppia come quella di un motore di induzione a tre fasi nella regione di velocità vicino a sincrona. Il fatto della coppia di inizio zero viene immediatamente osservato qui.
Il campo anteriore e il campo di reazione verso la parte posteriore del rotore, nonché lo sfondo nella parte posteriore e il campo di reazione anteriore del rotore si muovono in direzioni opposte con velocità relative di 2n producendo una seconda coppia armonica pulsata con un valore medio zero.
Di conseguenza, un motore a induzione monofase è un motore più rumoroso di un motore in 3 fasi che non ha una tale coppia pulsante. La coppia pulsante è in realtà una conseguenza diretta della potenza pulsante in un circuito a fase singola.
In effetti, nella caratteristica della velocità di coppia di un motore a induzione a fase singola, l’ordine di coppia rappresenta la coppia media.
Analisi semi-quantitativa:
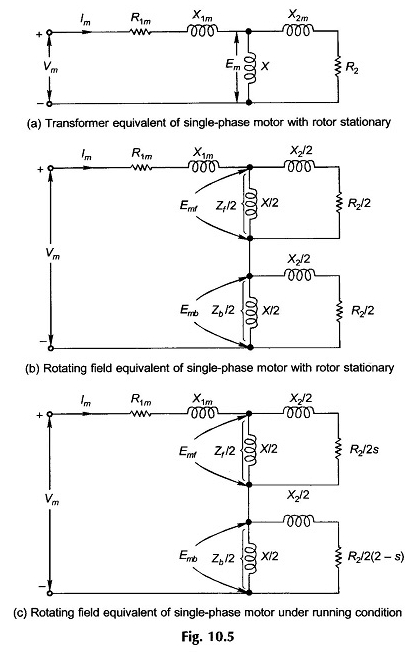
Per sviluppare il modello di circuito di un singolo motore a vacuum singolo su base semi-quantitativa, verranno utilizzati argomenti euristici. Il motore con un rotore stazionario agisce semplicemente come un trasformatore con un modello di circuito come mostrato in FIG.
10.5 (a), il ramo di core-dédoute è stato ignorato. Il suffisso M nello statore si riferisce all’avvolgimento principale e EM è l’EMF induce dallo statore configurato dal campo alternativo.
Il motore è ora visto dal punto di vista della teoria del campo rotante. L’EMF indotto risultante è costituito da due componenti uguali indotti dai due campi rotanti opposti della stessa resistenza, vale a dire
![]()
Le impedenze di magnetizzazione e rotore sono divise in due metà uguali collegate in serie, come mostrato nella Figura 10.5 (b); Il motore si comporta come due motori collegati nella serie A corrispondente a ciascun campo rotante.
I circuiti dei motori a due componenti sono identici allo stato stazionario perché il rotore ha lo stesso turno rispetto a ciascun campo rotante.
Quando il rotore funziona a velocità n rispetto al campo anteriore, lo spostamento è S rispetto ad esso e (2 – s) rispetto al campo rotante verso la parte posteriore in modo che il modello del circuito ora modifichi come nella Figura 10.5 (c).
Possiamo facilmente vedere da questa figura che ZF / 2 ≫ ZB / 2 e quindi EMF ≫ EMB, vale a dire che l’effetto del motore del campo anteriore predomina, creando un paio in corso.
Il bisogno pratico impone che i due campi rotanti siano progettati per avere una resistenza irregolare in condizioni stazionarie, che si auto-avviando auto-avviamento.
Ciò richiede un altro avvolgimento sul motore chiamato avvolgimento ausiliario che si trova nella quadratura spaziale con l’avvolgimento principale e include un numero minore di curve più sottili.
Questo avvolgimento può essere interrotto dal circuito una volta avviato il motore, tranne nel caso del motore gestito dal condensatore in cui può essere collegato al servizio di miglioramento per il fattore di potenza generale.
Analisi delle prestazioni:
Le prestazioni di un motore a induzione monofase possono essere ottenute mediante analisi del modello del circuito del motore riportato nella Figura 10.5 (c), come è stato fatto per un motore di induzione in tre fasi.
I risultati sono simili a quelli di un motore di induzione in tre fasi perché il modello di circuito è essenzialmente lo stesso.
I poteri di gap d’aria per i campi anteriori e posteriori sono forniti da

dove l’IM è la corrente di avvolgimento principale e RF e Rb sono le parti effettive delle impedenze del numero complesso Z̅F e Z̅B rispettivamente nella Figura 10.5 (c).
Le coppie prodotte da entrambi i campi possono essere espresse come

dove ωs = velocità sincrona in rad / s.
Poiché i due campi corrono in direzioni opposte, la coppia prodotta dai due si oppone. La coppia risultante sviluppata è quindi
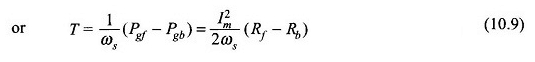
Le perdite di rame del rotore sono generalmente uguali ai tempi di scorrimento della potenza dell’aria. COSÌ
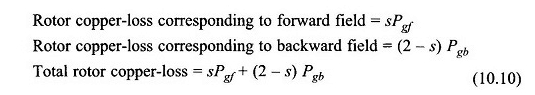
L’energia elettrica convertita in una forma meccanica lorda è

L’equazione (10.11) può anche essere scritta come
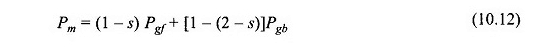
Ciò implica che l’ingresso di alimentazione elettrica al motore che trascura la perdita di rame dello statore è
![]()