Análise de mecanismo de indução de transição:
A utilidade da análise das condições operacionais de transição de um leitor, por exemplo, inicial, frenagem, mudança de carga, mudança de velocidade etc. já está explicada.
Uma análise rigorosa da operação de transição de uma unidade do motor de indução só pode ser realizada pelo modelo do eixo DQ envolvendo cálculos longos. Um método analítico simples, com precisão satisfatória para a maioria das aplicações, é obtida usando relacionamentos permanentes em casais.
Essa análise é baseada na hipótese de que as constantes de tempo elétrico podem ser negligenciadas, porque são muito pequenas em comparação com a constante de tempo mecânico. Assim, podemos escrever a seguinte equação para a análise de transição do treinamento de motores de indução:
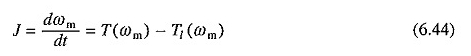
A equação (6.44) pode ser avaliada graficamente para obter a curva ωm vs t e as perdas de energia no motor e na resistência ao rotor externo usando o método já explicado.
Essa abordagem é geral e pode ser usada para qualquer análise transitória do mecanismo de indução, desde que sejam conhecidas as curvas de velocidade na velocidade permanente do motor [t (ω)] e a carga [t1 (ωm)]. Métodos analíticos aproximados são apresentados abaixo.
Iniciar e plug:
Para iniciar e conectar a operação da máquina, o torque é dado pela equação. (6.15). Substituindo da equação. (6.15) em (6.44) rendimentos
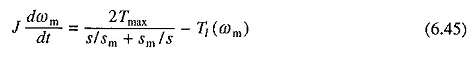
Em alguns casos, a equação. (6.45) estará em uma forma integrável e, portanto, pode ser resolvido analiticamente. É útil examinar transientes para iniciar e conectar operações ao operar sem carga. Assim, da equação. (6.45) para nenhuma operação de carregamento

Diferenciando a equação. (6.3) dá

Substituindo da equação. (6.47) em (6.46) e reorganizar os termos

τm é a constante de tempo mecânica do motor. É definido como o tempo gasto pelo motor para atingir sua velocidade síncrona de parada sob um torque acelerado constante igual ao torque máximo do motor.
Da equação. (6.48), o tempo necessário para iniciar um mecanismo de indução em qualquer carga é
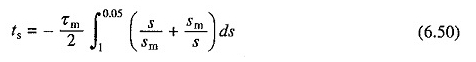
Durante a operação em nenhuma carga, o estado de equilíbrio é atingido quando S = 0. Assim, durante o início -Up, a mudança muda de 1 para 0. No entanto, se (6.50) for integrado para s = 1 a s = 0, um valor infinito é obtido para o tempo de início.
Como explicado, quando a velocidade final é a velocidade de equilíbrio no estado de equilíbrio, os transitorários são considerados maiores quando a faixa de velocidade de 95% é coberta. Portanto, na Eq. (6.50) A integração é realizada de s = 1 a s = 0,05. Resolução (6.50) fornece

Assim, o tempo de início depende do SM. O horário de início tem um valor mínimo de 1,22τm para sm = 0,4. Da equação. (6.12), quando RS é insignificante, a resistência ao rotor necessária para iniciar o motor pelo menos é

Da equação. (6.48), o tempo necessário para parar por conexão, quando ele é executado inicialmente a uma velocidade síncrona, pode ser expressa como
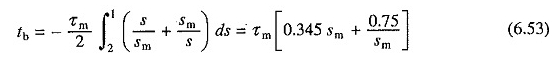
O tempo de inatividade é mais uma vez uma função do SM. Possui um valor mínimo de 1,027τm para sm = 1,47. O valor correspondente da resistência ao rotor é
![]()
Da mesma forma, da equação. (6.48), o tempo necessário para a reversão da velocidade conectando durante a execução em qualquer cobrança é dada por
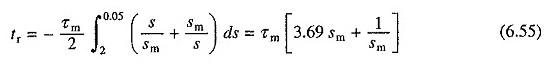
O tempo mínimo para a reversão é, portanto, 2,88τm e o valor correspondente de SM é 0,52. A resistência ao rotor necessária para a reversão da velocidade, conectando o tempo mínimo
![]()
Cálculo de perdas de energia:
Em seguida, vamos planejar as expressões para perda de energia nos enrolamentos do motor para iniciar e conectar operações. A perda de enrolamento do rotor para Start -Up pode ser escrita como

Substituindo equações. (6.5) e (6.11) dá

Como a máquina funciona sob qualquer carga

Substituindo da equação. (6.47)
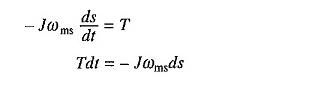
Ou
Substituto em (6.58) dá
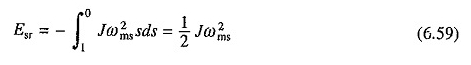
É interessante notar que a perda de energia do enrolamento do rotor é igual à energia cinética armazenada em peças móveis quando o processo de partida é concluído e é independente do tempo de partida ou da resistência ao rotor.
No entanto, se uma resistência externa estiver conectada no circuito do rotor, apenas parte dessa perda é usada para aquecer o motor. Perda de energia no enrolamento do estator, negligenciando a corrente de magnetização é

Portanto, a perda total de enrolamento durante a partida sob qualquer carga é

Prosseguir S Milady, a perda de enrolamento do rotor ao parar conectando -se sem carga

A equação (6.59) sugere que a perda de enrolamento do rotor pode ser reduzida quando começou a usar métodos com base na variação na velocidade síncrona. Por exemplo, considere um motor com um acordo para dobrar o número da postagem.
Deixe -o começar com um número de pólo mais alto para o qual a velocidade síncrona é ωms / 2. Então, de (6,59) a perda de cobre do rotor para a mudança de velocidade de 0 para ωMS / 2 será Jω2ms / 8. Agora, o número do polo será reduzido. Consequentemente, a perda de cobre do rotor para a faixa de velocidade ωms / 2 em ωms será
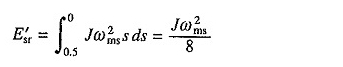
Assim, o enrolamento total do rotor é Jω2ms / 4, que é metade da perda de cobre quando não há disposição para dobrar o número do pólo.