Circuito de motor de indução equivalente:
Circuito do motor de indução equivalente – O comportamento da máquina de indução foi estudado em termos de fenômeno básico de campo. A tentativa aqui foi deliberadamente focada na analogia do transformador do motor de indução. Certos fatos estabelecidos até agora estão resumidos abaixo:
1 e 1
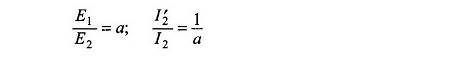
onde e2 = rotor do julgamento da EMF.
Além disso, os fluxos de I’2 para o terminal positivo dos fluxos E1 e I2 do terminal positivo de E2. Além disso, I2, como mostra o estator, é a corrente da frequência do estator F e está alinhada com o 2, o componente da corrente desenhada pelo estator para equilibrar o rotor MMF f2.
2. Como em um transformador, o componente de corrente de magnetização da IM da corrente do estator está atrasado atrás da EMF induzida pelo estator E1 de 90 °.
3. O mecanismo de indução não é apenas um transformador que altera a tensão e os níveis de corrente. Na verdade, ele se comporta como um transformador generalizado no qual a frequência também é transformada em proporção em slide, de modo que a EMF induz pelo rotor seja Se2 e a reatância do rotor é SX2.
O circuito equivalente ao mecanismo de indução agora pode ser desenhado pela fase, como na Figura 9.7 (a), na qual os elementos da série (agrupados) da resistência do estator e da reatância de vazamentos foram incluídos no modelo.
O transformador que conecta os circuitos do estator e do rotor é um transformador geral ideal no qual a tensão do rotor da parada E2 e a corrente do rotor I2 está ligada às quantidades do estator através da taxa de transformação A, enquanto o parâmetro de frequência aparece no circuito do rotor através do slissement S, um parâmetro mecânico. A potência de saída mecânica aparece na árvore indicada na figura.
O circuito do rotor pode ser referido ao lado do estator por um processo de dois etapas, modificando o circuito do rotor, para que a proporção de turno se torne a unidade e, em seguida, realizando uma transformação de frequência, o que resulta de um circuito de rotor equivalente à frequência do estator.
Ao multiplicar a tensão do rotor por A e a corrente do rotor por 1 / A, a impedância do rotor é modificada para
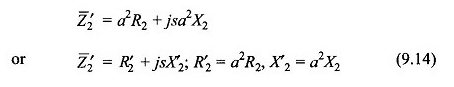
Nesta transformação, o poder permanece invariante. O circuito do rotor, depois de realizar esta etapa, é desenhado na Figura 9.7 (b). Isso reduz o rotor a um rotor equivalente com uma taxa de giro de unidade com o estator.
Do circuito do rotor equivalente à Figura 9.7 (b)

Divida o numerador e o denominador por S

Esta ponta simples se refere ao circuito do rotor na frequência do estator. O circuito do rotor modificado agora é desenhado na Figura 9.7 (c), no qual o circuito do rotor e do estator tem a mesma frequência, o transformador ideal agora é um transformador de proporção da unidade estacionária.
Também se percebe que, ao referir o circuito do rotor à frequência do estator, a reatância se torna constante (x’2) e a resistência se torna variável (R’2 / s). A transformação da equação. (9.15b) não é invariante (a tensão muda enquanto a corrente permanece a mesma).
A energia transferida para a escola secundária agora explica a perda de cobre do rotor e a potência mecânica (na forma elétrica). Isso contrasta com a Figura 9.7 (a) onde a energia mecânica é removida através de uma árvore.
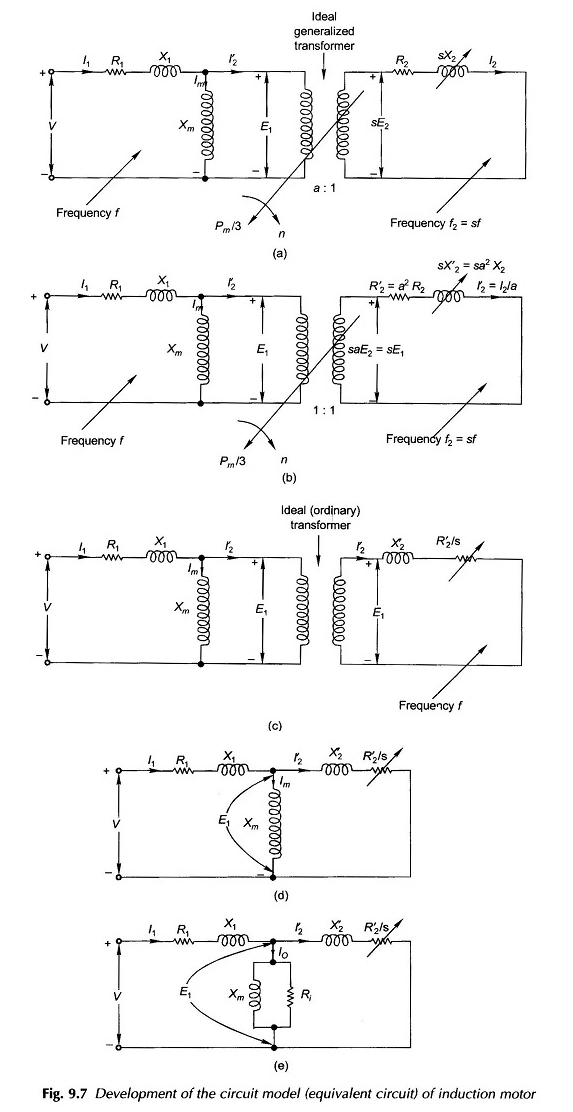
Na última etapa do desenvolvimento de circuitos motores de indução equivalentes, o transformador de razão da unidade ideal (comum) agora pode ser fornecido com o modelo de circuito na Figura 9.7 (d).
A representação da perda de ferro no estator pode ser introduzida heuristicamente no modelo de circuito da Figura 9.7 (d) colocando um RI de resistência paralelo ao XM como no modelo de circuito do transformador. Este circuito equivalente ao motor de indução é projetado na Figura 9.7 (e).
Se R’2, for separado de R’2 / S para representar a perda de cobre do rotor como uma entidade distinta, o modelo de circuito pode ser desenhado como na Figura 9.8 (a) na qual a resistência variável R’2 (1 / S – 1) representa a saída mecânica em forma elétrica. Alternativamente, o modelo de circuito da FIG.
9.8 (b) pode ser usado (isso corresponde à Figura 9.7 (d) na qual a resistência à perda de ferro LA é omitida e essa perda seria subtraída da saída mecânica bruta (potência absorvida por R’2 (1 / S – 1)).
Isso é equivalente a certas aproximações que são completamente aceitáveis na faixa de deslizamento normal em um mecanismo de indução. Além disso, os parâmetros deste circuito (que não precisam do valor do RI) podem ser facilmente obtidos por dois testes de não carga.
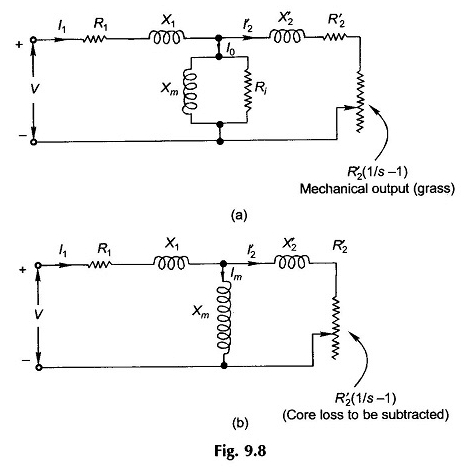
O modelo de circuito na Figura 9.8 (b) seria usado na maior parte da discussão a seguir. Podemos observar aqui que a energia dissipada em R’2 (1 / S – 1) inclui a perda básica, que deve ser subtraída para obter a potência mecânica bruta.
Para obter uma energia mecânica clara, a perda de vento e atrito deve ser mais subtraída. A perda básica e a perda de vento e a perda de atrito são agrupadas como uma perda de rotação, porque essas duas perdas ocorrem quando o motor está em funcionamento.
A perda de rotação em um motor de indução é significativamente constante a uma tensão aplicada constante e a velocidade do motor varia muito pouco da carga total em carga total.
Nota: energia mecânica líquida = potência da árvore