Circuito equivalente harmônico do mecanismo de indução:
Quando alimentado por um inversor ou por um cicloconetor, o controle do terminal do motor não é sinusoidal, mas possui uma simetria de meia onda. Uma forma de onda não -sinosoidal pode ser resolvida em componentes fundamentais e harmônicos usando a análise de Fourier.
Devido à simetria de meia onda, apenas os harmônicos estranhos estarão presentes. O circuito equivalente harmônico do motor de indução pode ser dividido em sequência positiva, sequência negativa e sequência zero.
Os harmônicos, que têm a mesma sequência de fases que a de fundamental, são chamados de harmônicos de sequência positiva. O circuito equivalente harmônico do mecanismo de indução com uma sequência de fases oposto ao fundamental é chamado harmônico de sequência negativa. Os harmônicos, que têm todas as tensões de três fases em fase, são chamados de harmônicos de sequência zero.
Considere os componentes da tensão da fase fundamental van = v1 sin ωt, vbn = v1 sin (ωt -2π / 3) e vcn = v1 sin (ωt – 4π / 3) com a sequência da fase ABC. As 5ª e a 7ª fase de fase correspondentes correspondentes são

As equações acima mostram que o 7º harmônico tem a sequência da fase ABC, que é a mesma do fundamental. É, portanto, um harmônico de sequência positiva. O 5º harmônico possui uma sequência de fases de ACB, por isso é um harmônico de sequência negativa.
Podemos mostrar que as tensões harmônicas e as correntes da ordem m = 6k + 1 (onde k é um número inteiro) são de sequência positiva e tensões harmônicas da ordem m = 6k – 1 são sequência negativa.
Da mesma forma, pode -se mostrar que os harmônicos da ordem m = 3k são sequência zero. Um harmônico de sequência positiva produzirá um campo rotativo, que se move na mesma direção que o fundamental a uma velocidade em vezes a do campo fundamental.
O campo rotativo semelhante produz por uma sequência negativa que o M harmônico se moverá na direção oposta à velocidade fundamental em sua velocidade. Componentes de sequência zero não produzem um campo rotativo.
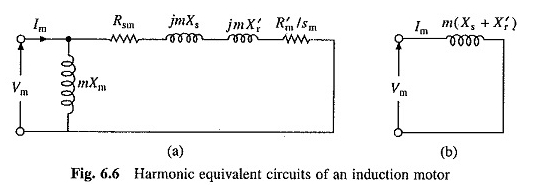
Para o componente fundamental, os circuitos equivalentes da Figura 6.1 serão aplicáveis. Para qualquer MTH harmônico, o circuito equivalente será como mostrado na Figura 6.6 (a). Cada reatância foi aumentada por um fator M. Devido aos efeitos da pele, os resistores também serão aumentados várias vezes. Escorregar SM para o MTH harmônico é dado por

O sinal negativo é aplicável a harmônicos que produzem campos rotativos para a frente e o sinal positivo para aqueles que produzem campos rotativos para trás. Como o SM está próximo da unidade, a resistência ((R′RN / SM)) tem um pequeno valor.
Como as reatâncias são muito grandes em comparação com os resistores, o circuito equivalente da Figura 6.6 (a) pode ser substituído pelo circuito simplificado na Figura 6.6 (b).
Quando alimentado de um conversor de semicondutores, pode -se mostrar que o torque líquido produzido por harmônicos é próximo de zero. Dado esse torque do motor, pode ser avaliado a partir de circuitos equivalentes na Figura 6.1 (b), usando a equação. (6.10), onde v é o componente fundamental da tensão de oferta.
O componente fundamental da corrente do rotor é obtido da equação. (6.4) e a corrente de harmônicos / Nth são calculados a partir da Figura 6.6 (b)

onde xs + x′r.
Geralmente, a oferta terá harmônicos estranhos. Quando o estator é Harmonics de Tripplen conectado à estrela (terceiro harmônico e seu múltiplo) não fluirá. A corrente do motor RMS IRMS será então

Quando o motor está conectado ao delta, os harmônicos de Trippplen circulam no delta, mas não fluem para a fonte. A corrente de origem pode, portanto, ser obtida multiplicando a ressonância magnética dada pela equação. (6.24) por √3. A corrente de fase do motor RMS será obtida por
![]()
Para um determinado torque e potência, a corrente RMS que flui no motor tem um valor mais alto. Além do efeito da pele, a resistência a rotores harmônicos tem um valor mais alto. Consequentemente, a presença de harmônicos aumenta consideravelmente a perda de cobre.
As perdas básicas também são aumentadas por harmônicos. Devido ao aumento de perdas, o motor deve ficar desapontado com o sentido de que a energia que pode ser obtida da máquina para o mesmo aumento da temperatura deve ser menor. A eficiência também é reduzida devido ao aumento de perdas.
Outro efeito importante dos alimentos não -sinoidal é a produção de casais pulsantes devido à interação entre o campo rotativo produzido por uma corrente harmônica e o rotor de outro harmônico. Harmonics 5, 7, 11 e 13 são os principais contribuintes para os pulsos de torque.
O 5º harmônico produz um campo rotativo para trás, enquanto o 7º harmônico produz um campo rotativo para a frente. Consequentemente, a velocidade relativa entre o campo produzida pelos harmônicos fundamentais e 5 e 7 é seis vezes a velocidade do fundamental.
Consequentemente, os pulsos de torque produzidos devido à interação das correntes harmônicas da 5ª e 7ª e do campo rotativo fundamental têm uma frequência seis vezes o fundamental.
Também pode ser demonstrado que os harmônicos 11 e 13 produzem pulsos de torque cuja frequência é 12 vezes o fundamental. Quando a frequência do suprimento do motor não é muito baixa, a frequência dos pulsos de torque é grande o suficiente para ser filtrada pela inércia do motor.
Consequentemente, as pulsações de torque não têm efeito significativo na velocidade do motor, embora aumentem o ruído e reduzem a vida útil do motor devido a vibrações. No entanto, quando a frequência do suprimento do motor é baixa, esses pulsos de torque causam pulsos de velocidade. O motor não se move suavemente, mas tem um movimento espumoso.