Dinamik İndüksiyon Motor Modelleme:
Genel olarak, herhangi bir makine için mekanik sabit, elektrik zaman sabitinden çok daha büyüktür. Sonuç olarak, indüksiyon motorunun dinamik modellemesi, sonuçların hassasiyeti kaybı olmadan elektrik geçişini ihmal ederek basitleştirilebilir.
İndüksiyon motoru devre modeli sabit bir kayma içindir, ancak genellikle motorun başlangıcında olduğu gibi yavaşça değişen bir kayma için uygulanır.
Şekil 9.64, dinamik indüksiyon motoru modellemesinin tipik tork kayma karakteristiğini (hızını) ve ayrıca kayanın (hız) bir fonksiyonu olarak yük torkunu göstermektedir.
Karakteristik (TL-S) üzerindeki her nokta, normal bir hızda çalıştıklarında yük ve motorun gerektirdiği torku (sürtünme) temsil eder. Motor yalnızca t> tl ise başlar ve t = tl’ye karşılık gelen ω0’ın düzenli bir çalışma hızına ulaşır, yani
İki tork hız özelliğinin kesişim noktası P. Rahatsızlık yöntemi ile p, belirtilen şarj hızının karakteristiği için kararlı bir çalışma noktası olduğu doğrulanabilir.
Herhangi bir nedenle, hız ω0, (t – tl) <0'dan büyük olursa, makine yükü kombinasyonu yavaşlar ve çalışma noktasına geri döner. Hız ω0'ın altına düşerse tam tersi oluşur.

Hızlanma döneminde

burada j = motorun birleşik ataleti ve yük. ŞİMDİ

Bu nedenle, Denk. (9.87)

Entegrasyon
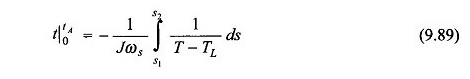
Çünkü 1 / (t – tl) terimi, denkleme doğrusal değildir, entegrasyondur. (9.89) S1 = 1 ve S2 = S0 durumunda Şekil 9.65’te gösterildiği gibi grafiksel (veya dijital olarak) gerçekleştirilmelidir.
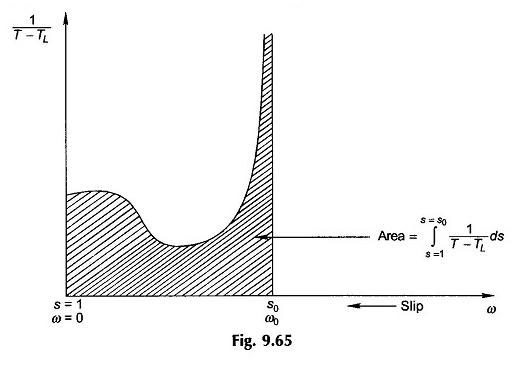
1 / (TL) ∞ ila S0 olduğundan, pratik entegrasyon istenen hassasiyete bağlı olarak sadece% 90 veya% 95’e kadar S0 gerçekleştirilir.
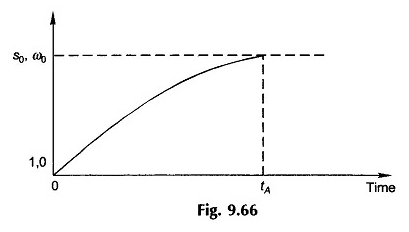
Şekil 9.66, hızlanma döneminde kayma (hız) zaman içinde nasıl değiştiğini göstermektedir. Vardiyanın bir fonksiyonu olarak (t – tl) ‘nin doğrusal olmaması nedeniyle, Şekil 9.66’daki kayma eğrisi (hız) üstel değildir.
Yük olmadan başlayarak (TL = 0):
Bu özel durumda, makinenin ve şarj sürtünme torkunun tl = 0 olduğu varsayılmaktadır.
Stator kayıplarının ihmal edilebilir olduğu varsayılarak (yani R1 = 0), denklemden elde edilen motor torku. (9.22)
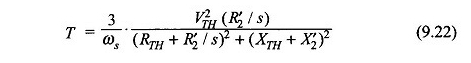
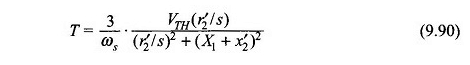
Ayrıca denklem. (9.24)
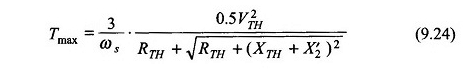

(Denk. (9.23))
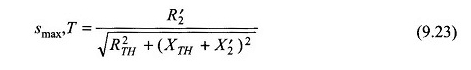

(9.90) ve (9.91) denklemlerinden,
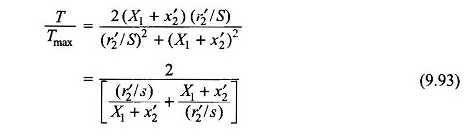
Denklemin yerine geçme. (9.92) (9.93)
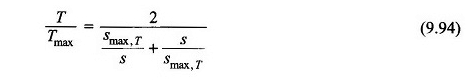
TL’nin sıfır olduğu varsayıldığından, motor torkunun kendisi hızlandırılmış tork,
Demek
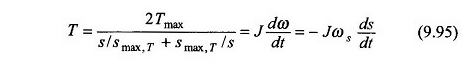
Denklemin entegrasyonu sırasında S1 vardiyasından S2’ye geçiş için Ti elde edilir. (9.95)
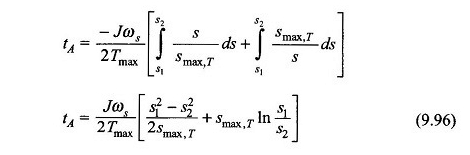
Makinenin başlangıç başlatma başlangıcına ulaşması için hızlanma süresi denklemden hesaplanabilir. (9.96) S1 = 1 ve S2 = S ile, yani

Optimal Smax, minimum hızlanma süresi için t:
S1, Denk. (9.96) Smax, T’den farklılaşmalı ve asimile edilmelidir. Verir

Makinenin başlangıçtan itibaren herhangi bir kaymaya ulaşması için minimum hızlanma süresi için, Smax’ın optimal değeri, t denklem tarafından verilir. (9.98) S1 = 1 ve S2 = S ile S. SO

Ve

Ayrıca, S1, Denk. (9.98) Denk. (9.92) Ver
