Geçiş İndüksiyon Motor Analizi:
Bir okuyucunun geçiş çalışma koşullarının analizinin yararlılığı, örneğin başlangıç, frenleme, yük değişikliği, hız değişimi vb. Zaten açıklanmıştır.
Bir indüksiyon motoru sürücüsünün geçiş çalışmasının titiz bir analizi, sadece uzun hesaplamaları içeren DQ ekseni modeli tarafından gerçekleştirilebilir. Çoğu uygulama için tatmin edici bir hassasiyete sahip basit bir analitik yöntem, kalıcı çift ilişkileri kullanılarak elde edilir.
Böyle bir analiz, elektrikli zaman sabitlerinin ihmal edilebileceği hipotezine dayanır, çünkü mekanik zaman sabitine kıyasla çok küçüktürler. Böylece, indüksiyon motoru eğitiminin geçiş analizi için aşağıdaki denklemi yazabiliriz:
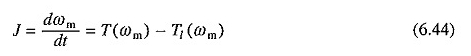
Denklem (6.44), ωm vs T eğrisini elde etmek için grafiksel olarak değerlendirilebilir ve zaten açıklanmış yöntem kullanılarak motor ve harici rotor direncindeki enerji kayıplarını elde edebilir.
Bu yaklaşım geneldir ve kalıcı motor hızında [t (ω)] hız hızı eğrileri ve [t1 (ωm)] yükü bilindiği sürece indüksiyon motorunun herhangi bir geçici analizi için kullanılabilir. Yaklaşık analitik yöntemler aşağıda sunulmaktadır.
Başla ve fiş:
Makinenin çalışmasını başlatmak ve bağlamak için tork denklemle verilir. (6.15). Denklemin yerine geçme. (6.15) (6.44) verim
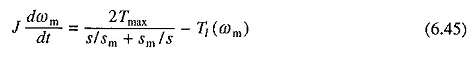
Bazı durumlarda, denklem. (6.45) entegre bir formda olacaktır ve bu nedenle analitik olarak çözülebilir. Yüksüz çalışırken işlemleri başlatma ve bağlama için geçişleri incelemek yararlıdır. Böylece, denklemin. (6.45) yükleme işlemi yok

Denklemin farklılaşması. (6.3) verir

Denklemin yerine geçme. (6.47) (6.46) ‘da ve terimleri yeniden düzenleyin

τm, motorun mekanik zaman sabitidir. Motorun, motorun maksimum torkuna eşit sabit bir hızlandırıcı tork altında eşzamanlı durma hızına ulaşmak için alınan zaman olarak tanımlanır.
Denklemin. (6.48), herhangi bir yükte bir indüksiyon motoru başlatmak için gereken süre
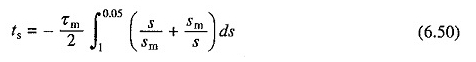
Yükleme işlemi sırasında, S = 0 olduğunda denge durumuna ulaşılır. Bu nedenle, başlangıç sırasında değişim 1’den 0’a değişir. Ancak, (6.50) s = 1 ila s = 0 için entegre edilirse, başlangıç süresi için sonsuz bir değer elde edilir.
Açıklandığı gibi, nihai hız denge durumundaki denge hızı olduğunda,% 95 hız aralığı kaplandığında geçici olarak daha yüksek olduğu düşünülmektedir. Bu nedenle, Denk. (6.50) Entegrasyon S = 1 ila S = 0.05 arasında gerçekleştirilir. Çözünürlük (6.50) verir

Böylece, başlangıç zamanı SM’ye bağlıdır. Başlangıç zamanının minimum değeri 1.22τm ila SM = 0.4’tür. Denklemin. (6.12), RS ihmal edilebilir olduğunda, motoru en azından başlatmak için gereken rotor direnci

Denklemin. (6.48), başlangıçta eşzamanlı bir hızda çalıştığında bağlantıya göre durmak için gereken süre,
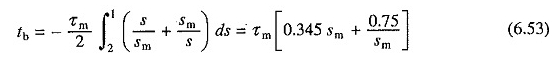
Kesinti süresi bir kez daha SM’nin bir fonksiyonudur. Minimum değeri 1.027τm ila SM = 1.47’dir. Rotora karşı dirençin karşılık gelen değeri
![]()
Aynı şekilde, denklemden. (6.48), herhangi bir şarj sırasında yürütme sırasında tıkanarak hızın tersine çevrilmesi için gereken süre,
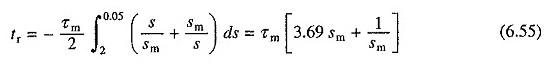
Bu nedenle tersine çevirme için minimum süre 2.88τm’dir ve SM’nin karşılık gelen değeri 0.52’dir. Minimum süreyi takarak hız tersine çevirme için gerekli rotor direnci
![]()
Enerji kayıplarının hesaplanması:
Ardından, başlangıç ve bağlantı işlemleri için motor sargılarındaki enerji kaybı ifadelerini planlayalım. Başlangıç için rotor sarma kaybı,

İkame denklemleri. (6.5) ve (6.11)

Makine herhangi bir yük altında çalışırken

Denklemin yerine geçme. (6.47)
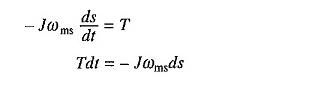
Veya
(6.58) ‘de ikame
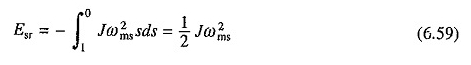
Rotor sargısının enerji kaybının, başlangıç işlemi tamamlandığında mobil parçalarda depolanan kinetik enerjiye eşit olduğunu ve kalkış süresinden veya rotor direncinden bağımsız olduğunu belirtmek ilginçtir.
Bununla birlikte, rotor devresine harici bir direnç bağlanırsa, motoru ısıtmak için bu kaybın sadece bir kısmı kullanılır. Stator sargısında enerji kaybı, mıknatıslanma akımını ihmal etmek

Bu nedenle, herhangi bir yük altında başlangıç sırasındaki toplam sarma kaybı

Milady’ye devam edin, yüksüz takarak dururken rotorun sarılmasının kaybı şu şekilde yazılabilir.

Denklem (6.59), rotor sarma kaybının, senkron hızdaki değişime dayanarak yöntemler kullanmaya başladığında azaltılabileceğini düşündürmektedir. Örneğin, posta numarasını ikiye katlamak için bir düzenlemeye sahip bir motoru düşünün.
Senkron hızın ωms / 2 olduğu daha yüksek bir kutup numarası ile başlayın. Daha sonra, (6.59) ‘dan 0’dan ωms / 2’ye hız değişimi için rotorun bakır kaybı JΩ2ms / 8 olacaktır. Şimdi, kutup numarası düşürülür. Sonuç olarak, ωms’deki hız aralığı ωms / 2 için rotorun bakır kaybı
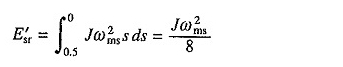
Böylece, rotorun toplam sargısı JΩ2ms / 4’tür, bu da kutup sayısını ikiye katlamak için hiçbir hüküm olmadığında bakır kaybının yarısıdır.