Analyse transitoire du moteur à induction:
L’utilité de l’analyse des conditions de fonctionnement transitoires d’un lecteur, par exemple le démarrage, le freinage, la modification de la charge, le changement de vitesse, etc. est déjà expliquée.
Une analyse rigoureuse du fonctionnement transitoire d’un entraînement moteur à induction ne peut être effectuée que par le modèle de l’axe DQ impliquant de longs calculs. Une méthode d’analyse simple, avec une précision satisfaisante pour la plupart des applications, est obtenue en utilisant des relations de couple en régime permanent.
Une telle analyse est basée sur l’hypothèse que les constantes de temps électrique peuvent être négligées, car elles sont très petites par rapport à la constante de temps mécanique. Ainsi, nous pouvons écrire l’équation suivante pour l’analyse transitoire de l’entraînement moteur à induction:
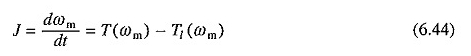
L’équation (6.44) peut être évaluée graphiquement pour obtenir la courbe ωm vs t et les pertes d’énergie dans la résistance moteur et rotor externe en utilisant la méthode déjà expliquée.
Cette approche est générale et peut être utilisée pour toute analyse transitoire du moteur d’induction tant que les courbes de vitesse de vitesse en régime permanent du moteur [T (ωm)] et de la charge [t1 (ωm)] sont connues. Des méthodes analytiques approximatives sont présentées ci-dessous.
Démarrage et bouchage:
Pour démarrer et brancher le fonctionnement de la machine, le couple est donné par l’équation. (6.15). Se substituant à partir de l’équation. (6.15) en (6,44) rendements
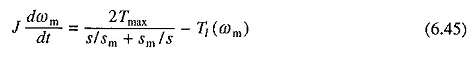
Dans certains cas, l’équation. (6.45) sera sous une forme intégrable et peut donc être résolue analytiquement. Il est utile d’examiner les transitoires pour le démarrage et le branchement des opérations lors du fonctionnement sans charge. Ainsi, de l’équation. (6.45) pour aucune opération de chargement

Différenciant l’équation. (6.3) donne

Se substituant à partir de l’équation. (6.47) dans (6.46) et réorganiser les termes

τm est la constante de temps mécanique du moteur. Il est défini comme le temps pris par le moteur pour atteindre sa vitesse synchrone de l’arrêt sous un couple accélérant constant égal au couple maximal du moteur.
De l’équation. (6.48), le temps nécessaire pour démarrer un moteur à induction sur aucune charge est
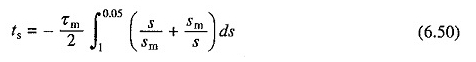
Lors du fonctionnement sur aucune charge, l’état d’équilibre est atteint lorsque S = 0. Ainsi, pendant le démarrage, les changements de glissement de 1 à 0. Cependant, si (6,50) est intégré pour S = 1 à S = 0, une valeur infinie est obtenue pour l’heure de début.
Comme expliqué, lorsque la vitesse finale est la vitesse d’équilibre à l’état d’équilibre, les transitoires sont considérés comme supérieurs lorsque la plage de vitesse de 95% est couverte. Par conséquent, en Eq. (6.50) L’intégration est effectuée de S = 1 à S = 0,05. La résolution (6,50) donne

Ainsi, l’heure de début est fonction de SM. L’heure de début a une valeur minimale de 1,22τm à SM = 0,4. De l’équation. (6.12), lorsque RS est négligeable, la résistance au rotor requise pour démarrer le moteur au minimum est

De l’équation. (6.48), le temps requis pour s’arrêter par branchement, lorsqu’il s’exécute initialement à une vitesse synchrone, peut être exprimé comme
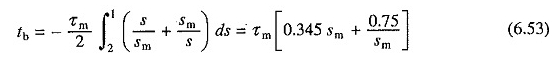
Le temps d’arrêt est à nouveau fonction de SM. Il a une valeur minimale de 1,027τm à SM = 1,47. La valeur correspondante de la résistance au rotor est
![]()
De même, à partir de l’équation. (6.48), le temps requis pour l’inversion de la vitesse en se branchant lors de l’exécution sur aucune charge n’est donné par
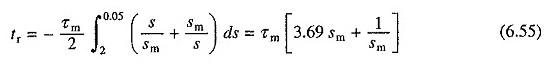
Le temps minimum pour l’inversion est donc de 2,88τm et la valeur correspondante de SM est de 0,52. La résistance au rotor requise pour l’inversion de la vitesse en branchant le temps minimum est
![]()
Calcul des pertes d’énergie:
Prévoyons ensuite les expressions pour la perte d’énergie dans les enroulements du moteur pour le démarrage et le branchement des opérations. La perte d’enroulement du rotor pour le démarrage peut être écrite comme

Substituant des équations. (6.5) et (6.11) donne

Comme la machine fonctionne sous aucune charge

Se substituant à partir de l’équation. (6.47)
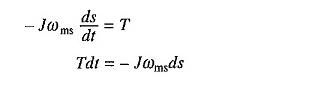
ou
Substituer dans (6,58) donne
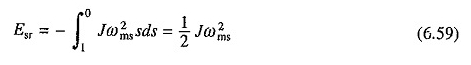
Il est intéressant de noter que la perte d’énergie de l’enroulement du rotor est égale à l’énergie cinétique stockée en pièces mobiles à l’achèvement du processus de départ, et elle est indépendante de l’heure de départ ou de la résistance au rotor.
Cependant, si une résistance externe est connectée dans le circuit du rotor, seule une partie de cette perte est utilisée pour chauffer le moteur. La perte d’énergie dans l’enroulement du stator, négligeant le courant de magnétisation est

Par conséquent, la perte totale d’enroulement pendant le démarrage sous aucune charge est

Procéder S Milady, la perte d’enroulement du rotor lors de l’arrêt en branchant sans charge peut être écrite comme

L’équation (6.59) suggère que la perte d’enroulement du rotor peut être réduite lorsqu’elle a commencé en utilisant des méthodes basées sur la variation de la vitesse synchrone. Par exemple, considérons un moteur avec un arrangement pour doubler le numéro de poteau.
Laissez-le démarrer avec un numéro de pôle plus élevé pour lequel la vitesse synchrone est ωms / 2. Ensuite, à partir de (6,59) la perte de cuivre du rotor pour le changement de vitesse de 0 à ωms / 2 sera Jω2ms / 8. Maintenant, le numéro de pôle est abaissé. Par conséquent, la perte de cuivre du rotor pour la plage de vitesse Ωms / 2 à ωms sera
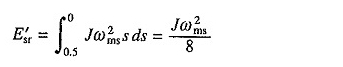
Ainsi, la perte totale d’enroulement du rotor est JΩ2ms / 4, qui est la moitié de la perte de cuivre lorsqu’il n’y a aucune disposition pour doubler le numéro de pôle.