Circuit équivalent à moteur à induction:
Circuit équivalent à moteur à induction – Le comportement de la machine à induction a été étudié en termes de phénomène de base de champ. La tentative ici était délibérément axée sur l’analogie du transformateur du moteur d’induction. Certains faits établis jusqu’à présent sont résumés ci-dessous:
1 et 1
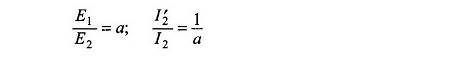
où E2 = Rotor de l’arrêt EMF.
De plus, I’2 s’écoule dans la borne positive de E1 et I2 s’écoule de la terminale positive de E2. De plus, I2, comme le montre le stator est le courant de la fréquence du stator F et est en phase avec I’2, le composant du courant dessiné par le stator pour équilibrer le rotor MMF F2.
2. Comme dans un transformateur, le composant de courant magnétisant IM du courant du stator est à la traîne de l’EMF induit par le stator E1 de 90 °.
3. Le moteur à induction n’est pas simplement un transformateur qui modifie la tension et les niveaux de courant. Il se comporte en fait comme un transformateur généralisé dans lequel la fréquence est également transformée en proportion pour glisser de telle sorte que l’EMF induit par le rotor soit SE2 et la réactance du rotor est SX2.
Le circuit équivalent à moteur d’induction peut désormais être dessiné par phase comme sur la figure 9.7 (a) dans laquelle les éléments de la série (regroupés) de la résistance du stator et de la réactance des fuites ont été inclus dans le modèle.
Le transformateur reliant les circuits du stator et du rotor est un transformateur généralisé idéal dans lequel la tension du rotor de l’arrêt E2 et le courant du rotor I2 sont liés aux quantités du stator via le rapport de transformation A, tandis que le paramètre de fréquence apparaît dans le circuit du rotor à travers le glissement S, un paramètre mécanique. La puissance de sortie mécanique apparaît sur l’arbre indiqué sur la figure.
Le circuit du rotor peut être référé sur le côté stator par un processus en deux étapes modifiant le circuit du rotor afin que le ratio de virage devienne l’unité puis effectuant une transformation de fréquence, ce qui résulte d’un circuit de rotor équivalent à la fréquence du stator.
En multipliant la tension du rotor par A et le courant du rotor par 1 / A, l’impédance du rotor est modifiée pour
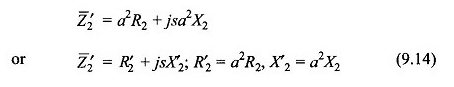
Dans cette transformation, le pouvoir reste invariant. Le circuit du rotor, après avoir effectué cette étape, est dessiné sur la figure 9.7 (b). Cela réduit le rotor à un rotor équivalent ayant un ratio de virage d’unité avec le stator.
À partir du circuit de rotor équivalent de la figure 9.7 (b)

Diviser à la fois le numérateur et le dénominateur par S

Cette astuce simple fait référence au circuit du rotor à la fréquence du stator. Le circuit de rotor modifié est maintenant dessiné sur la figure 9.7 (c) dans laquelle le circuit du rotor et du stator a la même fréquence, le transformateur idéal est désormais un transformateur de rapport unitaire stationnaire.
Il est également remarqué qu’en référant le circuit du rotor à la fréquence du stator, la réactance devient constante (x’2) et la résistance devient variable (R’2 / S). La transformation de l’équation. (9.15b) n’est pas invariant de puissance (changements de tension tandis que le courant reste le même).
La puissance transférée au secondaire explique désormais à la fois la perte de cuivre du rotor et la puissance mécanique (sous forme électrique). Ceci contraste avec la figure 9.7 (a) où la puissance mécanique est enlevée via un arbre.
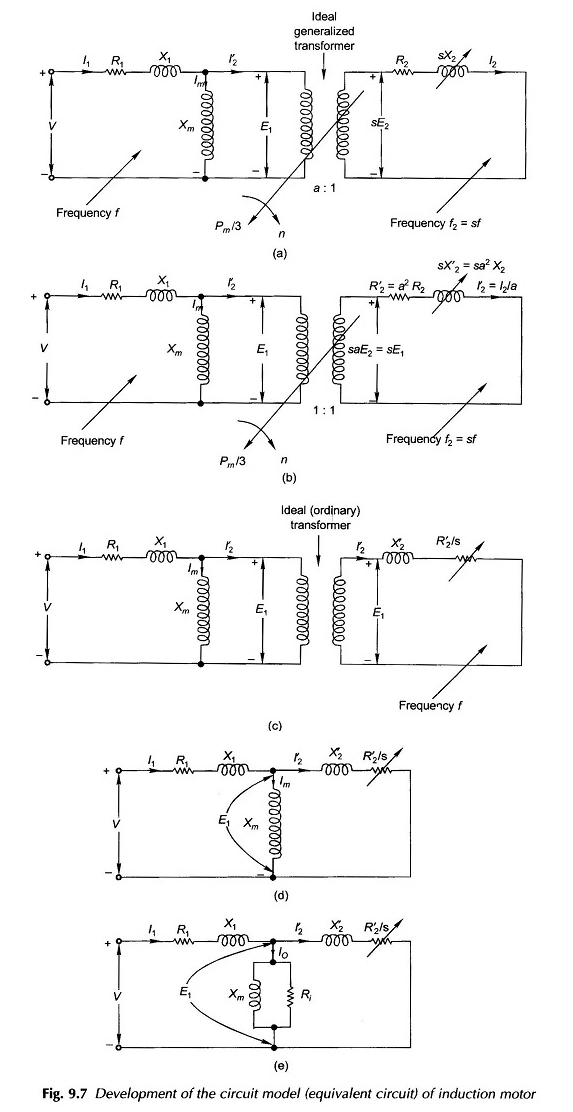
À la dernière étape du développement de circuits équivalents à moteur à induction, le transformateur de rapport unitaire idéal (ordinaire) peut désormais être dispensé avec le modèle de circuit de la figure 9.7 (d).
La représentation de la perte de fer dans le stator peut être introduite heuristiquement dans le modèle de circuit de la figure 9.7 (d) en plaçant une résistance RI parallèle avec XM comme dans le modèle de circuit du transformateur. Ce circuit équivalent à moteur à induction est dessiné sur la figure 9.7 (e).
Si R’2, est séparé de R’2 / s pour représenter la perte de cuivre du rotor comme une entité distincte, le modèle de circuit peut être dessiné comme sur la figure 9.8 (a) dans laquelle la résistance variable R’2 (1 / s – 1) représente la sortie mécanique sous forme électrique. Alternativement, le modèle de circuit de la Fig.
9.8 (b) pourrait être utilisé (cela correspond à la figure 9.7 (d) dans laquelle la résistance à la perte de fer RI est omise et cette perte serait soustraite de la sortie mécanique brute (puissance absorbée par R’2 (1 / s – 1)).
Cela équivaut à certaines approximations qui sont tout à fait acceptables dans la plage normale de glissement dans un moteur à induction. De plus, les paramètres de ce circuit (qui n’ont pas besoin de la valeur de RI) peuvent être facilement obtenus par deux tests de non-chargement.
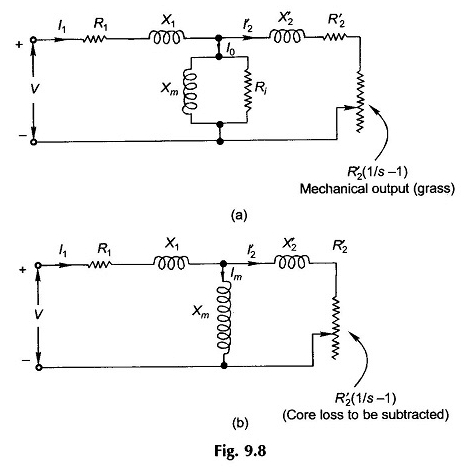
Le modèle de circuit de la figure 9.8 (b) serait utilisé pour la majeure partie de la discussion qui suit. On peut noter ici que la puissance dissipée en R’2 (1 / s – 1) comprend la perte de base, qui doit être soustraite pour obtenir la puissance mécanique brute.
Pour obtenir une puissance mécanique nette, la perte de vent et de frottement doit être soustraite davantage. La perte de base et la perte de vent et la perte de frottement sont regroupées comme une perte de rotation car ces deux pertes se produisent lorsque le moteur est en cours d’exécution.
La perte de rotation dans un moteur à induction est sensiblement constante à une tension appliquée constante et la vitesse du moteur varie très peu de la pleine charge à pleine charge.
Remarque: puissance mécanique nette = puissance de l’arbre