Circuito equivalente armónico del motor de inducción:
Cuando está alimentado por un inversor o un cicloconectivo, el control del terminal motor no es sinusoidal, pero tiene una simetría de media onda. Una forma de onda no sinusoidal se puede resolver en componentes fundamentales y armónicos utilizando el análisis de Fourier.
Debido a la simetría de media onda, solo habrá armónicos extraños. El circuito equivalente armónico del motor de inducción se puede dividir en secuencia positiva, secuencia negativa y secuencia cero.
Los armónicos, que tienen la misma secuencia de fases que la de fundamental, se denominan armónicos de secuencia positiva. El circuito armónico equivalente del motor de inducción que tiene una secuencia de fases opuestas a fundamental se llama armónica de secuencia negativa. Los armónicos, que tienen las tres tensiones de fase en fase, se denominan armónicos de secuencia cero.
Considere los componentes de voltaje de fase fundamental van = v1 sin ωt, vbn = v1 sen (ωt -2π / 3) y vcn = v1 sen (ωt – 4π / 3) con la secuencia de fase ABC. Las tensiones de fase armónica de 5º y 7º y 7º correspondiente son

Las ecuaciones anteriores muestran que el séptimo armónico tiene la secuencia de fase ABC, que es la misma que la de fundamental. Por lo tanto, es un armónico de secuencia positiva. El quinto armónico tiene una secuencia de fases ACB, por lo que es un armónico de secuencia negativa.
Podemos mostrar que las tensiones armónicas y las corrientes del orden M = 6k + 1 (donde K es un entero) son de secuencia positiva y tensiones armónicas del orden M = 6k – 1 son secuencia negativa.
Del mismo modo, se puede demostrar que los armónicos del orden M = 3k son secuencia cero. Un armónico de secuencia positiva producirá un campo rotativo, que se mueve en la misma dirección que el fundamental a una velocidad m veces que el campo fundamental.
El campo rotativo similar produce por una secuencia negativa, el armónico M se moverá en la dirección opuesta a la velocidad fundamental a su velocidad. Los componentes de secuencia cero no producen un campo rotativo.
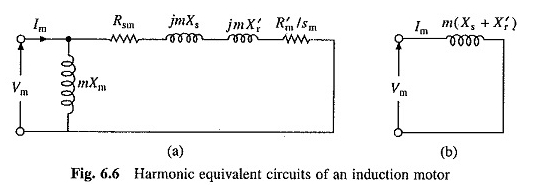
Para el componente fundamental, los circuitos equivalentes de la Figura 6.1 serán aplicables. Para cualquier MTH armónico, el circuito equivalente será como se muestra en la Figura 6.6 (a). Cada reactancia se ha incrementado por un factor M. Debido a los efectos de la piel, las resistencias también aumentarán varias veces. Deslizar SM para el MTH armónico está dado por

El signo negativo es aplicable a los armónicos que producen campos rotativos hacia adelante y el signo positivo para aquellos que producen campos rotativos al revés. Como SM está cerca de la unidad, la resistencia ((R′RN / SM)) tiene un valor pequeño.
Como las reactancias son muy grandes en comparación con las resistencias, el circuito equivalente de la Figura 6.6 (a) puede ser reemplazado por el circuito simplificado en la Figura 6.6 (b).
Cuando se alimenta desde un convertidor de semiconductores, se puede demostrar que el par neto producido por armónicos está cerca de cero. Dado este par motor, se puede evaluar a partir de circuitos equivalentes en la Figura 6.1 (b), utilizando la ecuación. (6.10), donde V es el componente fundamental del voltaje de suministro.
El componente fundamental de la corriente del rotor se obtiene de la ecuación. (6.4) y la corriente armónica / enésima se calculan a partir de la Figura 6.6 (b)

donde xs + x′r.
En general, el suministro tendrá armónicos extraños. Cuando el estator sea tripplen, los armónicos conectados a la estrella (tercer armónico y su múltiplo) no fluirán. La corriente del motor RMS IRMS será entonces

Cuando el motor está conectado al delta, los armónicos de Tripplen circulan en el delta, pero no fluirán hacia la fuente. Por lo tanto, la corriente fuente se puede obtener multiplicando la resonancia magnética dada por la ecuación. (6.24) por √3. La corriente de fase del motor RMS se obtendrá por
![]()
Para un par dado y potencia de potencia, la corriente RMS que fluye en el motor tiene un valor más alto. Además, debido al efecto de la piel, la resistencia a los rotores armónicos tiene un valor más alto. En consecuencia, la presencia de armónicos aumenta considerablemente la pérdida de cobre.
Las pérdidas básicas también aumentan por los armónicos. Debido al aumento de las pérdidas, el motor debe decepcionarse en el sentido de que la potencia que se puede obtener de la máquina para el mismo aumento de la temperatura debe ser menor. La eficiencia también se reduce debido al aumento de las pérdidas.
Otro efecto importante de los alimentos no minúsculos es la producción de parejas pulsantes debido a la interacción entre el campo rotativo producido por una corriente armónica y el rotor de otro armónico. Harmonics 5, 7, 11 y 13 son los principales contribuyentes a los pulsos de torque.
El quinto armónico produce un campo rotativo hacia atrás, mientras que el 7º armónico produce un campo rotativo hacia adelante. En consecuencia, la velocidad relativa entre el campo producido por los armónicos fundamentales y 5 y 7 es seis veces la velocidad de fundamental.
En consecuencia, los pulsos de torque producidos debido a la interacción de las corrientes armónicas 5 y 7 y el campo rotativo fundamental tienen una frecuencia seis veces lo fundamental.
También se puede demostrar que los armónicos 11 y 13 producen pulsos de par cuya frecuencia es 12 veces la fundamental. Cuando la frecuencia del suministro del motor no es muy baja, la frecuencia de los pulsos de torque es lo suficientemente grande como para ser filtrada por inercia del motor.
En consecuencia, las pulsaciones de par no tienen un efecto significativo en la velocidad del motor, aunque aumentan el ruido y reducen la vida útil del motor debido a las vibraciones. Sin embargo, cuando la frecuencia del suministro del motor es baja, estos pulsos de par causan pulsos de velocidad. El motor no se mueve suavemente sino que tiene un movimiento desigual.