Muestra paso a paso como obtener esta ecuacion del circuito equivalente por fas…
Circuito de motor de inducción equivalente:
Circuito de motor de inducción equivalente: el comportamiento de la máquina de inducción se ha estudiado en términos de fenómeno básico de campo. El intento aquí se centró deliberadamente en la analogía del transformador de motor de inducción. Ciertos hechos establecidos hasta ahora se resumen a continuación:
1 y 1
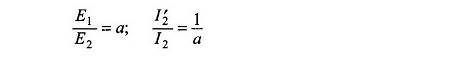
donde e2 = rotor del juicio EMF.
Además, I’2 fluye hacia el terminal positivo de E1 e I2 fluye del terminal positivo de E2. Además, i2, como muestra el estator, es la corriente de la frecuencia del estator F y está en línea con el 2, el componente de la corriente dibujada por el estator para equilibrar el rotor MMF F2.
2. Como en un transformador, el componente de corriente de magnetización de IM de la corriente del estator se retrasa detrás del EMF inducido por el estator E1 de 90 °.
3. El motor de inducción no es solo un transformador que cambia el voltaje y los niveles de corriente. En realidad, se comporta como un transformador generalizado en el que la frecuencia también se transforma en proporción para deslizarse para que el EMF induce por el rotor es SE2 y la reactancia del rotor es SX2.
El circuito equivalente al motor de inducción ahora se puede dibujar por fase como en la Figura 9.7 (a) en el que los elementos de la serie (agrupados) de la resistencia del estator y la reactancia de las fugas se incluyeron en el modelo.
El transformador que conecta los circuitos del estator y el rotor es un transformador general ideal en el que el voltaje del rotor de la parada E2 y la corriente del rotor i2 están vinculadas a las cantidades del estator a través de la relación de transformación A, mientras que el parámetro de frecuencia aparece en el circuito del rotor a través del slissement S, un parámetro mecánico. La potencia de salida mecánica aparece en el árbol indicada en la figura.
El circuito del rotor se puede referir al lado del estator mediante un proceso de dos pasos que modifica el circuito del rotor para que la relación de giro se convierta en la unidad y luego realice una transformación de frecuencia, lo que resulta de un circuito de rotor equivalente a la frecuencia de la estator.
Al multiplicar el voltaje del rotor por A y la corriente del rotor por 1 / A, la impedancia del rotor se modifica para
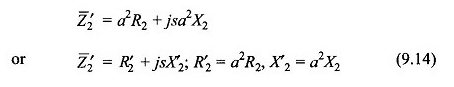
En esta transformación, el poder sigue siendo invariante. El circuito del rotor, después de haber llevado a cabo este paso, se dibuja en la Figura 9.7 (b). Esto reduce el rotor a un rotor equivalente con una relación de giro de la unidad con el estator.
Desde el circuito del rotor equivalente a la Figura 9.7 (b)

Divide tanto el numerador como el denominador por s

Esta punta simple se refiere al circuito del rotor en la frecuencia del estator. El circuito del rotor modificado ahora se dibuja en la Figura 9.7 (c) en el que el rotor y el circuito del estator tienen la misma frecuencia, el transformador ideal es ahora un transformador de relación de unidad estacionaria.
También se nota que al referir el circuito del rotor a la frecuencia del estator, la reactancia se vuelve constante (x’2) y la resistencia se vuelve variable (r’2 / s). La transformación de la ecuación. (9.15b) no es potencia invariante (los cambios de tensión mientras la corriente sigue siendo la misma).
La potencia transferida a la escuela secundaria ahora explica tanto la pérdida de cobre del rotor como la potencia mecánica (en forma eléctrica). Esto contrasta con la Figura 9.7 (a) donde la potencia mecánica se elimina a través de un árbol.
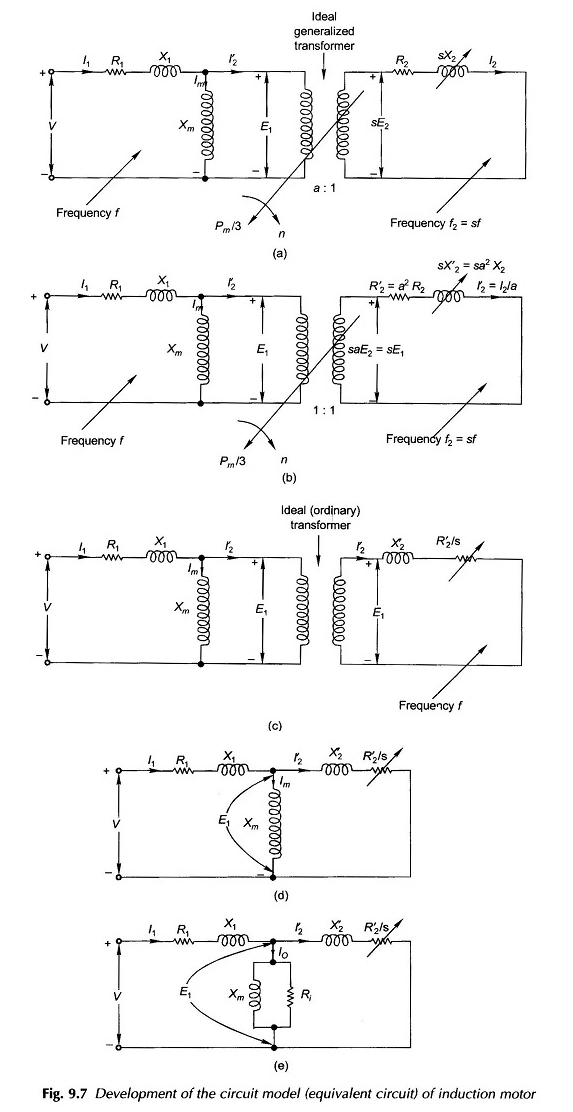
En la última etapa del desarrollo de circuitos de motor de inducción equivalentes, el transformador de relación unitaria ideal (ordinario) ahora puede proporcionar el modelo de circuito en la Figura 9.7 (d).
La representación de la pérdida de hierro en el estator se puede introducir heurísticamente en el modelo de circuito de la Figura 9.7 (d) colocando una resistencia RI paralela con XM como en el modelo de circuito del transformador. Este circuito equivalente al motor de inducción está diseñado en la Figura 9.7 (e).
Si R’2, se separa de R’2 / S para representar la pérdida de cobre del rotor como una entidad distinta, el modelo de circuito se puede dibujar como en la Figura 9.8 (a) en la que la resistencia variable R’2 (1 / S – 1) representa la salida mecánica en forma eléctrica. Alternativamente, el modelo de circuito de la Fig.
9.8 (b) podría usarse (esto corresponde a la Figura 9.7 (d) en la que se omite la resistencia a la pérdida de hierro LA y esta pérdida se restará de la salida mecánica bruta (potencia absorbida por R’2 (1 / S – 1)).
Esto es equivalente a ciertas aproximaciones que son completamente aceptables en el rango de deslizamiento normal en un motor de inducción. Además, los parámetros de este circuito (que no necesitan el valor RI) pueden obtenerse fácilmente mediante dos pruebas sin carga.
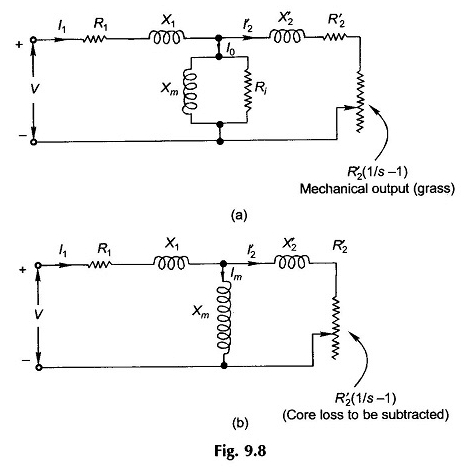
El modelo de circuito en la Figura 9.8 (b) se utilizaría para la mayor parte de la siguiente discusión. Podemos observar aquí que la potencia se disipó en R’2 (1 / S – 1) incluye la pérdida básica, que debe restarse para obtener la potencia mecánica bruta.
Para obtener una potencia mecánica clara, la pérdida de viento y fricción debe ser más restado. La pérdida básica y la pérdida de viento y la pérdida de fricción se agrupan como una pérdida de rotación porque estas dos pérdidas ocurren cuando el motor está funcionando.
La pérdida de rotación en un motor de inducción es significativamente constante para un voltaje aplicado constante y la velocidad del motor varía muy poco a partir de la carga completa a plena carga.
Nota: Potencia mecánica neta = Potencia del árbol