El convertidor de frecuencia a longitud de onda calcula la longitud de onda correspondiente a una frecuencia determinada en el vacío.
Esta herramienta es esencial para ingenieros de RF, diseñadores de antenas e investigadores que trabajan en la propagación de ondas electromagnéticas.
Fórmula utilizada
La conversión se basa en la relación fundamental entre la velocidad de la luz, la frecuencia y la longitud de onda:
λ = c/f
O :
λ es la longitud de onda en metros (m),
es la velocidad de la luz en el vacío (≈ 299 792 458 m/s),
f es la frecuencia en hercios (Hz).
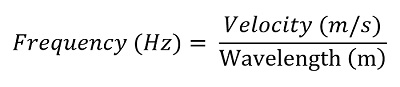
Explicación de la fórmula.
Esta ecuación muestra que la longitud de onda es inversamente proporcional a la frecuencia.
Cuanto mayor es la frecuencia, más corta es la longitud de onda.
Esto permite comprender el comportamiento de las señales en diferentes entornos, en particular en la comunicación inalámbrica, el radar o la óptica.
Usar
Este cálculo se utiliza en aplicaciones de transmisión de radio, diseño de antenas, microondas y fibra óptica.
Ayuda a determinar las dimensiones físicas necesarias para que un dispositivo funcione a una frecuencia determinada.
Ejemplo de cálculo
Si la frecuencia f = 3 GHz :
λ = 299.792.458 / (3 × 10⁹) = 0,0999 m
Por tanto, la longitud de onda correspondiente es de aproximadamente 0,1 m (10 cm).
Consejos de cálculo
- Verifique que la frecuencia ingresada sea positiva y esté correctamente expresada (Hz, kHz, MHz o GHz).
- Para medios distintos al vacío, utilice la velocidad de propagación correspondiente (v = c / √εr).
- Los valores de alta frecuencia darán longitudes de onda muy pequeñas, útiles en electrónica u óptica.
¿Por qué hacer esta conversión?
Convertir una frecuencia en una longitud de onda nos permite comprender el tamaño físico asociado con la señal.
Esta información es fundamental para el diseño de antenas, el cálculo de resonancias o la planificación de radioenlaces.
Beneficios
- Le permite vincular directamente la frecuencia y la dimensión física de las ondas.
- Útil para sistemas RF, microondas, ópticos e inalámbricos.
- Facilita el ajuste de antenas y circuitos resonantes.
Resultado esperado: una correspondencia clara entre la frecuencia de una señal y su longitud de onda asociada.