Modelado de motor de inducción dinámica:
En general, la constante mecánica para cualquier máquina es mucho mayor que la constante de tiempo eléctrico. En consecuencia, el modelado dinámico del motor de inducción se puede simplificar descuidando la transición eléctrica sin ninguna pérdida de precisión de los resultados.
El modelo de circuito del motor de inducción es para un deslizamiento constante, pero también se aplicaría a un deslizamiento lentamente que varía, como generalmente es el caso en el inicio del motor.
La Figura 9.64 muestra la característica de deslizamiento de par típica (velocidad) del modelado de motor de inducción dinámica y también el par de carga en función del deslizamiento (velocidad).
Cada punto en la característica (TL-S) representa el par (fricción) requerido por la carga y el motor cuando funcionan a una velocidad regular. El motor solo comenzaría si t> tl y alcanzaría una velocidad de funcionamiento regular de ω0 que corresponde a t = tl, es decir
El punto de intersección P de las dos características de velocidad de par. El método de perturbación puede verificar que P es un punto de operación estable para la característica de la velocidad de carga indicada.
Si por alguna razón, la velocidad se vuelve mayor que Ω0, (t – tl) <0, la combinación de carga de la máquina desacelera y regresa al punto de operación. Lo contrario ocurre si la velocidad disminuye por debajo de ω0.

Durante el período de aceleración

donde j = inercia combinada del motor y la carga. AHORA

Por lo tanto, la ecuación. (9.87) modificado a

Integración
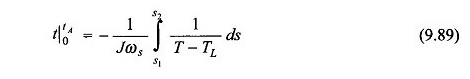
Dado que el término 1 / (t – tl) es no lineal, integración en la ecuación. (9.89) debe realizarse gráficamente (o digitalmente) como se muestra en la Figura 9.65 para el caso cuando S1 = 1 y S2 = S0.
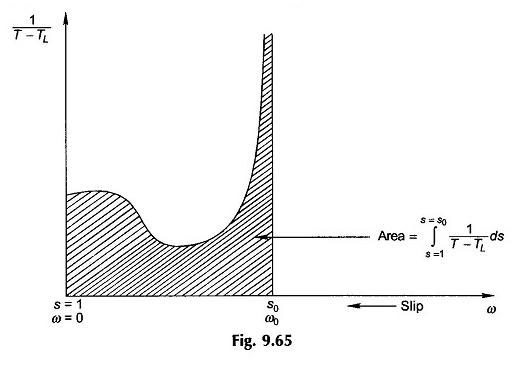
Dado que 1 / (TL) se convierte en ∞ a S0, la integración práctica solo se lleva a cabo hasta 90 o 95% S0 dependiendo de la precisión deseada.
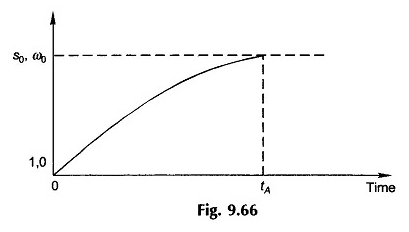
La Figura 9.66 muestra cómo el deslizamiento (velocidad) varía con el tiempo durante el período de aceleración que alcanza el valor regular de S0 (ω0) en el tiempo, el tiempo de aceleración. Debido a la no linealidad de (T – TL) en función del cambio, la curva deslizante (velocidad) en la Figura 9.66 no es exponencial.
Comenzando sin carga (TL = 0):
En este caso particular, se supone que la máquina y el par de la fricción de carga TL = 0.
Suponiendo que las pérdidas del estator son insignificantes (es decir, R1 = 0), el par del motor obtenido de la ecuación. (9.22) es
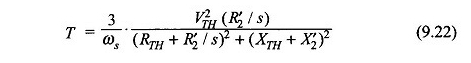
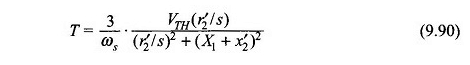
También de la ecuación. (9.24)
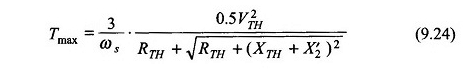

a un cambio en (Ec. (9.23))
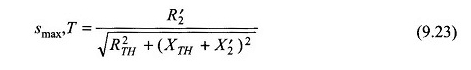

De las ecuaciones (9.90) y (9.91),
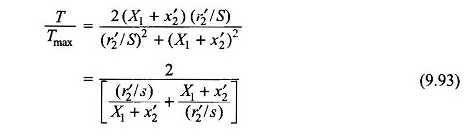
Sustituyendo la ecuación. (9.92) en (9.93)
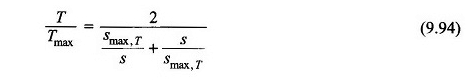
Dado que se supone que TL es cero, el par del motor en sí es el par acelerado,
Eso es decir
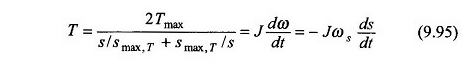
Ti para cambiar de cambio S1 a S2 se obtiene durante la integración de la ecuación. (9.95) como
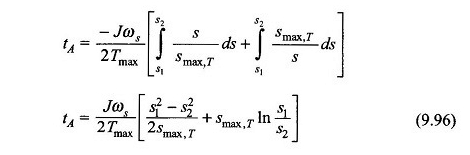
El tiempo de aceleración para que la máquina alcance el inicio regular del inicio, se puede calcular a partir de la ecuación. (9.96) con S1 = 1 y S2 = S, es decir

SMAX óptimo, t para un tiempo de aceleración mínimo:
Para encontrar el valor óptimo de SMAX, T para el modelado de motor de inducción dinámica para tener un tiempo de aceleración mínimo para llegar a S2 desde S1, Eq. (9.96) debe diferenciarse de SMAX, T y asimilarse a cero. Dio

Para un tiempo de aceleración mínimo para que la máquina alcance cualquier deslizamiento desde el inicio, el valor óptimo de SMAX, T viene dado por la ecuación. (9.98) con S1 = 1 y S2 = S. entonces

Y

Además, para permitirnos calcular el valor óptimo de la resistencia del rotor para acelerar la máquina para deslizar S2 de S1, Eq. (9.98) se sustituye en la ecuación. (9.92) Dar
