Motor de inducción de una sola fase:
Un motor de inducción de una sola fase incluye un devanado distribuido de fase única en el estator y el rotor de ardilla normal, como se ilustra esquemáticamente en la Figura 10.1 en la que, por conveniencia, el devanado del estator se ilustra en forma concentrada.

Hay dos métodos importantes para analizar este motor, a saber
- Teoría del campo transversal y
- Teoría de los campos rotativos.
Como este último se parece más a la teoría de la máquina de inducción de tres fases avanzada anteriormente, se adoptará aquí.
Campo pulsante como dos campos giratorios:
La Figura 10.1 proporciona el esquema esquemático de un motor de inducción monofásico con un devanado del estator y un rotor de jaula de ardilla. El devanado se distribuye en el espacio para que el espacio fundamental de MMF sea el componente más dominante de la distribución real de MMF.
Los armónicos espaciales de MMF, como en el caso de un motor de inducción en tres fases, serían ignorados. Cuando el devanado lleva una corriente sinusoidal, produce un MMF distribuido al espacio sinusoidalmente cuyo valor máximo de pulsado con el tiempo. Como muestra el eje del devanado, el MMF en cualquier ángulo θ es
![]()
donde θ es el ángulo medido desde el eje del devanado. AHORA
![]()
para que el MMF tenga una distribución del espacio y el tiempo expresado
![]()
Esta ecuación puede ser manipulada trigonométrica en la forma
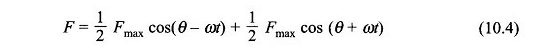
La ecuación (10.4) nos dice que un campo de fase monofásica pulsado puede considerarse como una superposición de dos campos rotativos que se ejecutan a una velocidad sincrónica (Ω = 2πf elegido. Rad / s) en direcciones opuestas:

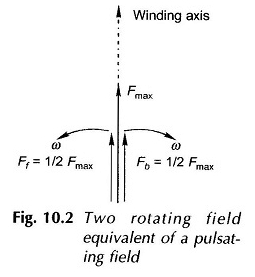
Estos dos campos tienen una amplitud igual a (1/2) Fmax donde Fmax es el valor máximo del pulsatorio MMF a lo largo del eje del devanado. La división de un solo campo pulsado en dos campos rotativos que se ejecuta en direcciones opuestas se ilustra en la Figura 10.2.
Esta figura muestra la ubicación de los campos rotativos en un momento en que el MMF a lo largo del eje de devanado es + Fmax.
Deslizamiento del rotor en comparación con dos campos giratorios:

Para el caso único ilustrado en la Figura 10.1, la Figura 10.3 muestra los campos rotativos hacia adelante y hacia atrás con el rotor que funciona a la velocidad N en la dirección del campo frontal. El cambio del rotor con respecto al campo rotativo hacia adelante FF es entonces

Mientras que el rotor se desliza con respecto al campo de giro -back FB

Por lo tanto, los portaobjetos del rotor en comparación con los dos campos rotativos son diferentes y están dados por las ecuaciones (10.5a) y (10.5b).
Característica de la velocidad del motor del motor de inducción de una sola fase:
Tratamiento cualitativo en un estado de rotor estacionario (n = 0, es decir, S = 1), los dos campos rotativos se deslizan frente al rotor con el mismo cambio, s = 1, (ver ecuaciones (10.5a) y (10.5b)) inducen corrientes iguales en el rotor de la ardilla.
Los dos campos rotativos tienen la misma resistencia y producen parejas iguales y opuestas, lo que conduce a un par inicial neto de valor cero. Por lo tanto, el motor de inducción de un solo vacío único es un arranque no profesional.
Además, los dos campos rotativos inducen un EMF que resulta en el estator que equilibra la tensión aplicada al suponer una baja impedancia de fuga del devanado del estator.
Sin embargo, si el rotor está diseñado para funcionar a la velocidad N en la dirección del campo frontal, los dos cambios ahora son S y (2 – s).
Para la operación normal (2 – s) ≫ s y, por lo tanto, las corrientes del rotor inducidas por el fondo son mucho más altas que cuando se detienen y tienen un factor de potencia más bajo.
El rotor opuesto correspondiente MMF, en presencia de la impedancia del estator, conduce a una reducción considerablemente del campo a la parte trasera. Por otro lado, el campo rotativo hacia el cambio bajo induce corrientes más pequeñas de un factor de potencia más alto en el rotor que cuando se detiene.
Esto conduce a una gran mejora en la onda de flujo frontal.
Esta reducción del campo a la parte trasera y el fortalecimiento del campo frontal depende del cambio y la diferencia aumenta a medida que se reduce la inclinación S (en comparación con el campo frontal) o la velocidad del rotor en la dirección delantera se acerca a la velocidad sincrónica.
De hecho, cerca de la velocidad sincrónica, el campo frontal puede ser el campo varias veces. Como resultado, hay una pareja neta. Los dos campos siempre deben inducir el devanado del EMF del estator para equilibrar la tensión aplicada.
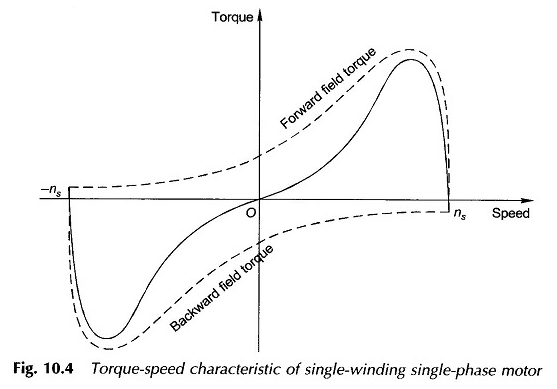
La característica completa de la velocidad del torque como la suma de las dos características de velocidad de par (delantera y posterior) se dibuja en la Figura 10.4.
El resultado del debilitamiento de un campo y el refuerzo simultáneo de los otros conduce a una característica de la velocidad del par, como la de un motor de inducción de tres fases en la región de velocidad cerca de Sincronous. El hecho del par de inicio cero se observa inmediatamente aquí.
El campo frontal y el campo de reacción hacia la parte trasera del rotor, así como el fondo hacia la parte trasera y el campo de reacción delantero del rotor se mueven en direcciones opuestas con velocidades relativas de 2n produciendo un segundo torque pulsado armónico con un valor promedio cero.
En consecuencia, un motor de inducción de una sola fase es un motor más ruidoso que un motor de 3 fases que no tiene tal par pulsante. El par pulsante es, de hecho, una consecuencia directa de la potencia pulsante en un circuito de una sola fase.
De hecho, en la característica de la velocidad de torque de un motor de inducción de una sola fase, el orden de par representa el par promedio.
Análisis semicuantitativo:
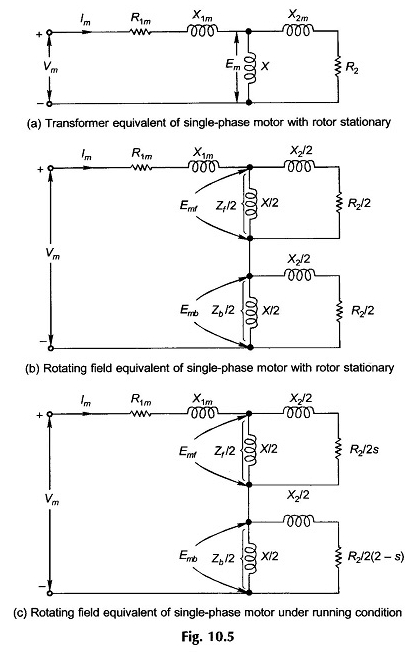
Para desarrollar el modelo de circuito de un solo motor de vacío único sobre una base semicuantitativa, se utilizarán argumentos heurísticos. El motor con un rotor estacionario actúa simplemente como un transformador con un modelo de circuito como se muestra en la Fig.
10.5 (a), la rama de Core-Dédoute ha sido ignorada. El sufijo M en el estator se refiere al devanado principal y EM es el EMF induce por el estator configurado por el campo alternativo.
El motor ahora se ve desde el punto de vista de la teoría del campo rotativo. El EMF inducido resultante está compuesto por dos componentes iguales inducidos por los dos campos rotativos opuestos de la misma resistencia, es decir, es decir
![]()
Las impedancias de magnetización y rotor se dividen en dos mitades iguales conectadas en serie como se muestra en la Figura 10.5 (b); El motor se comporta como dos motores conectados en la Serie A correspondiente a cada campo rotativo.
Los circuitos de los dos motores componentes son idénticos al estado estacionario porque el rotor tiene el mismo cambio en comparación con cada campo rotativo.
Cuando el rotor funciona a la velocidad N en comparación con el campo frontal, el cambio es S en comparación con él y (2 – s) en comparación con el campo rotativo hacia la parte trasera para que el modelo de circuito ahora se modifique como en la Figura 10.5 (c).
Podemos ver fácilmente en esta figura que ZF / 2 ≫ ZB / 2 y, por lo tanto, EMF ≫ EMB, es decir, el efecto del motor del campo frontal predomina, creando un par en progreso.
La necesidad práctica dicta que los dos campos rotativos están diseñados para tener una resistencia desigual en condiciones estacionarias, que se inician a sí mismos.
Esto requiere un devanado más en el motor llamado devanado auxiliar que está en cuadratura espacial con el devanado principal e incluye un número menor de giros más delgados.
Este devanado se puede cortar del circuito una vez que el motor ha comenzado, excepto en el caso del motor administrado por el condensador donde puede vincularse al servicio de mejora para el factor de potencia general.
Análisis de rendimiento:
El rendimiento de un motor de inducción de una sola fase se puede obtener mediante el análisis del modelo de circuito del motor dado en la Figura 10.5 (c), como se hizo para un motor de inducción en tres fases.
Los resultados son similares a los de un motor de inducción en tres fases porque el modelo de circuito es esencialmente el mismo.
Los poderes de gafa de aire para los campos delanteros y traseros están dados por

Donde IM es la corriente principal de devanado y RF y RB son las partes reales de las impedancias del número complejo Z̅F y Z̅B respectivamente en la Figura 10.5 (c).
Las parejas producidas por ambos campos pueden expresarse como

donde Ωs = velocidad sincrónica en rad / s.
Dado que los dos campos corren en direcciones opuestas, la pareja producida por los dos se opone. La pareja resultante desarrollada es, por lo tanto,
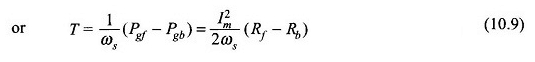
Las pérdidas de cobre del rotor son generalmente iguales a los tiempos deslizantes de la potencia del aire. Entonces
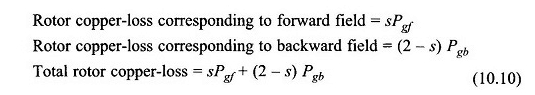
La potencia eléctrica convertida en una forma mecánica grave es

La ecuación (10.11) también se puede escribir como
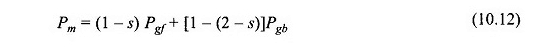
Esto implica que la entrada de suministro eléctrico al motor que descuida la pérdida de cobre del estator es
![]()