Modélisation dynamique du moteur à induction:
En général, le constant mécanique pour toute machine est beaucoup plus grand que la constante de temps électrique. Par conséquent, la modélisation dynamique du moteur d’induction peut être simplifiée en négligeant le transitoire électrique sans aucune perte de précision des résultats.
Le modèle de circuit du moteur à induction tient pour un glissement constant, mais s’appliquerait également pour un glissement variant lentement comme c’est généralement le cas dans le démarrage du moteur.
La figure 9.64 montre la caractéristique typique de glissement de couple (vitesse) d’une modélisation dynamique du moteur d’induction et également le couple de charge en fonction du glissement (vitesse).
Chaque point sur la caractéristique (TL-S) représente le couple (frottement) exigé par la charge et le moteur lorsqu’ils fonctionnent à une vitesse régulière. Le moteur ne démarrerait que si t> tl et atteindrait une vitesse de fonctionnement régulière de ω0 qui correspond à t = tl, c’est-à-dire
Le point d’intersection P des deux caractéristiques de vitesse de couple. Il peut être vérifié par la méthode de perturbation selon laquelle P est un point de fonctionnement stable pour la caractéristique de la vitesse de charge indiquée.
Si pour une raison quelconque, la vitesse devient supérieure à ω0, (t – tl) <0, la combinaison de charge de machine décélère et revient au point de fonctionnement. L’inverse se produit si la vitesse diminue en dessous de ω0.

Pendant la période d’accélération

où j = inertie combinée du moteur et de la charge. Maintenant

Par conséquent, Eq. (9.87) modifie à

Intégration
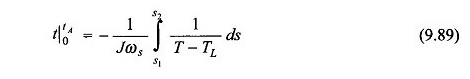
Puisque, le terme 1 / (t – tl) est non linéaire, l’intégration dans l’équation. (9.89) doit être effectué graphiquement (ou numériquement) comme le montre la figure 9.65 pour le cas lorsque S1 = 1 et S2 = S0.
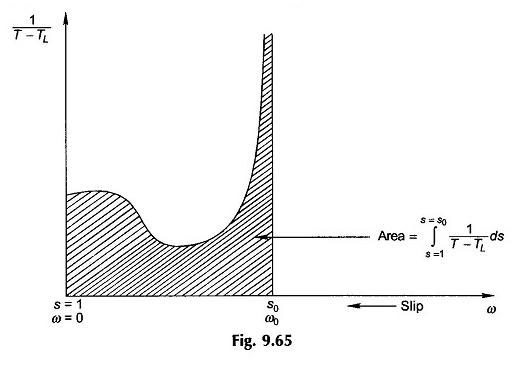
Étant donné que 1 / (t – tl) devient ∞ à S0, l’intégration pratique n’est effectuée que jusqu’à 90 ou 95% de S0 en fonction de la précision souhaitée.
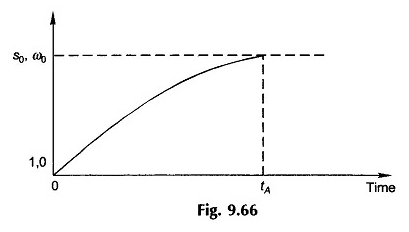
La figure 9.66 montre comment le glissement (vitesse) varie avec le temps pendant la période d’accélération atteignant la valeur régulière de S0 (ω0) dans le temps TA, le temps d’accélération. En raison de la non-linéarité de (T – TL) en fonction du glissement, la courbe de glissement (vitesse) de la figure 9.66 n’est pas exponentielle.
En commençant sur sans charge (tl = 0):
Dans ce cas particulier, il est supposé que la machine et le couple de frottement de charge tl = 0.
En supposant que les pertes de stator soient négligeables (c’est-à-dire R1 = 0), le couple moteur obtenu à partir de l’équation. (9.22) est
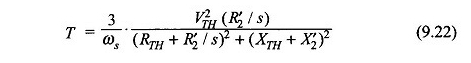
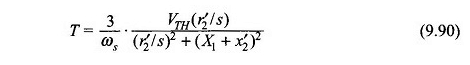
Également de l’équation. (9.24)
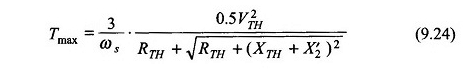

à un glissement de (Eq. (9.23))
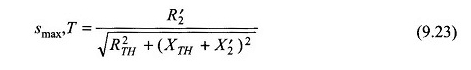

À partir des équations (9,90) et (9,91),
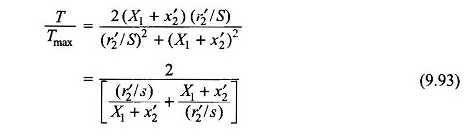
Substituant l’équation. (9.92) dans (9.93)
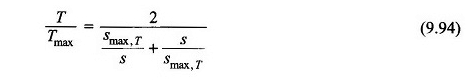
Étant donné que TL est supposé nul, le couple moteur lui-même est le couple accéléré,
c’est-à-dire
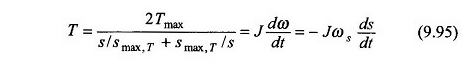
Le temps TA pour passer du glissement S1 à S2 est obtenu lors de l’intégration de l’équation. (9.95) comme
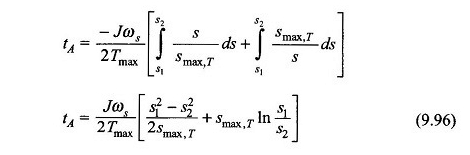
Le temps d’accélération pour que la machine atteigne la vitesse régulière du démarrage peut être calculée à partir de l’équation. (9.96) avec S1 = 1 et S2 = S, c’est-à-dire

SMAX optimal, t pour le temps d’accélération minimum:
Pour trouver la valeur optimale de SMAX, T pour la modélisation dynamique du moteur d’induction pour avoir un temps d’accélération minimum pour atteindre S2 à partir de S1, Eq. (9.96) Doit être différencié par rapport à SMAX, T et assimilé à zéro. Cela donne

Pour un temps d’accélération minimum pour que la machine atteigne tout glissement à partir du début, la valeur optimale de SMAX, T est donnée par l’équation. (9.98) avec S1 = 1 et S2 = S. Alors

et

De plus, pour nous permettre de calculer la valeur optimale de la résistance au rotor pour accélérer la machine pour glisser S2 de S1, Eq. (9.98) est substitué en Eq. (9.92) Donner
