Moteur à induction monophasé:
Un moteur à induction monophasé comprend un enroulement distribué monophasé sur le stator et le rotor d’écureuil normal, comme illustré schématiquement sur la figure 10.1 dans laquelle pour la commodité, l’enroulement du stator est illustré sous forme concentrée.

Il existe deux méthodes importantes pour analyser ce moteur, à savoir
- Théorie du champ transversal et
- Théorie des champs rotatifs.
Comme ce dernier s’apparente davantage à la théorie de la machine à induction triphasée avancée plus tôt, elle sera adoptée ici.
Champ pulsant comme deux champs rotatifs:
La figure 10.1 donne le schéma schématique d’un moteur à induction monophasé avec un enroulement stator et un rotor d’écureuil-cage. L’enroulement est distribué dans l’espace afin que l’espace fondamental de MMF soit la composante la plus dominante de la distribution MMF réelle.
Les harmoniques spatiales de MMF, comme dans le cas d’un moteur à induction en trois phases, seraient alors ignorées. Lorsque l’enroulement porte un courant sinusoïdal, il produit un MMF distribué à l’espace sinusoïdalement dont la valeur de pic pulsate avec le temps. Comme le montre l’axe de l’enroulement, le MMF à n’importe quel angle θ est
![]()
où θ est l’angle mesuré à partir de l’axe d’enroulement. Maintenant
![]()
de sorte que le MMF a à la fois une distribution d’espace et de temps exprimée
![]()
Cette équation peut être manipulée trigonométrique dans la forme
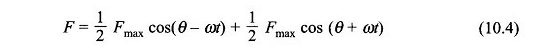
L’équation (10.4) nous dit qu’un champ monophasé pulsé peut être considéré comme une superposition de deux champs rotatifs tournant à une vitesse synchrone (ω = 2πf élu. RAD / S) dans des directions opposées:

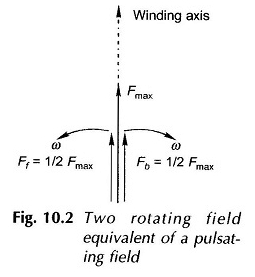
Ces deux champs ont une amplitude égale à (1/2) fmax où Fmax est la valeur maximale du MMF pulsatoire le long de l’axe de l’enroulement. Le fractionnement d’un seul champ pulsé en deux champs rotatifs tournant dans des directions opposées est illustrée sur la figure 10.2.
Cette figure montre l’emplacement des champs rotatifs au moment où le MMF le long de l’axe d’enroulement est + FMAX.
Glissement du rotor par rapport à deux champs rotatifs:

Pour le boîtier unique illustré sur la figure 10.1, la figure 10.3 montre les champs rotatifs vers l’avant et vers l’arrière avec le rotor qui tourne à la vitesse n en direction du champ avant. Le glissement du rotor par rapport au champ rotatif vers l’avant FF est alors

tandis que le rotor glisse par rapport au champ tournant vers l’arrière FB

Ainsi, le rotor glisse par rapport aux deux champs rotatifs est différent et sont donnés par les équations (10,5a) et (10,5b).
Caractéristique de la vitesse du couple du moteur à induction monophasé:
Traitement qualitatif dans un état de rotor stationnaire (n = 0, c’est-à-dire S = 1), les deux champs rotatifs glissent devant le rotor au même glissement, S = 1, (voir Eqs (10,5A) et (10,5b)) induire des courants égaux dans le rotor de l’écureau.
Les deux champs rotatifs ont la même résistance et produisent des couples égaux et opposés, ce qui entraîne un couple de démarrage net de la valeur nulle. Le moteur à induction monophasé à vide unique est donc un démarrage non-propre.
De plus, les deux champs rotatifs induisent un EMF résultant dans le stator qui équilibre la tension appliquée en supposant une faible impédance de fuite de l’enroulement du stator.
Si, cependant, le rotor est conçu pour fonctionner à vitesse n dans le sens du champ avant, les deux glissements sont désormais S et (2 – S).
Pour le fonctionnement normal (2 – S) ≫ S et, par conséquent, les courants de rotor induits par le champ vers l’arrière sont beaucoup plus importants qu’à l’arrêt et ont un facteur de puissance inférieur.
Le rotor adverse correspondant MMF, en présence de l’impédance du stator, entraîne une réduction considérablement du champ vers l’arrière. D’un autre côté, le champ rotatif vers l’avant à faible glissement induit des courants plus petits d’un facteur de puissance plus élevé dans le rotor qu’à l’arrêt.
Cela conduit à une grande amélioration dans la vague de flux avant.
Cette réduction du champ vers l’arrière et le renforcement du champ avant dépend du glissement et la différence augmente à mesure que le glissement S (par rapport au champ avant) réduit ou la vitesse du rotor dans le sens avant devient proche de la vitesse synchrone.
En fait, à proximité de la vitesse synchrone, le champ avant peut être plusieurs fois le champ vers l’arrière. En conséquence, il y a un couple de course net. Les deux champs doivent toujours induire l’EMF enroulement du stator pour équilibrer la tension appliquée.
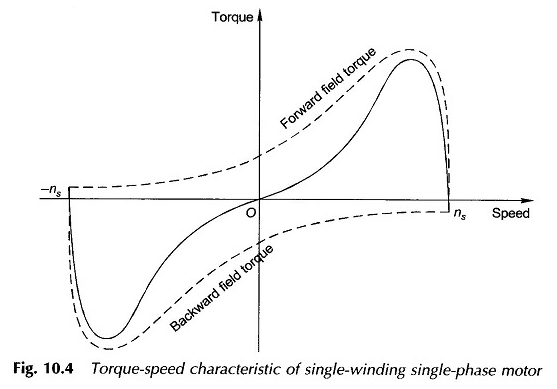
La caractéristique complète de la vitesse de couple comme la somme des deux caractéristiques de vitesse de couple (avant et vers l’arrière) est dessinée sur la figure 10.4.
Le résultat de l’affaiblissement d’un champ et du renforcement simultané de l’autre conduit à une caractéristique de vitesse de couple comme celle d’un moteur d’induction en trois phases dans la région de vitesse proche du synchrone. Le fait du couple de démarrage zéro est immédiatement observé ici.
Le champ avant et le champ de réaction vers l’arrière du rotor ainsi que le champ vers l’arrière et le champ de réaction avant du rotor se déplacent dans des directions opposées avec des vitesses relatives de 2N produisant un deuxième couple pulsé harmonique avec une valeur moyenne nulle.
En conséquence, un moteur à induction monophasé est un moteur le plus bruyant qu’un moteur à 3 phases qui n’a pas un tel couple pulsant. Le couple pulsant est en fait une conséquence directe de la puissance pulsante dans un circuit monophasé.
En fait, dans la caractéristique de la vitesse de couple d’un moteur à induction monophasé, l’ordonnée de couple représente le couple moyen.
Analyse semi-quantitative:
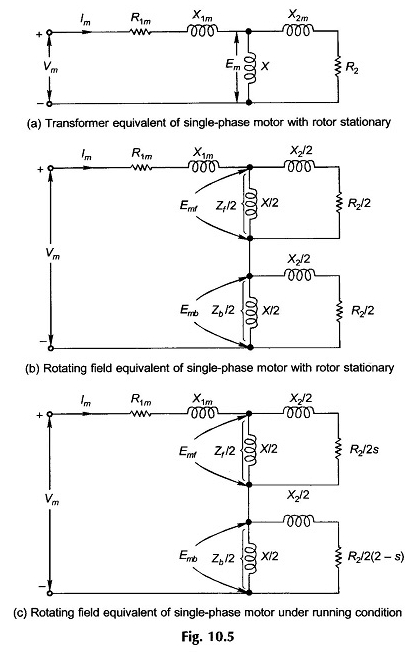
Pour développer le modèle de circuit d’un moteur monophasé à vide unique sur une base semi-quantitative, des arguments heuristiques seront utilisés. Le moteur avec un rotor stationnaire agit simplement comme un transformateur avec un modèle de circuit comme le montre la Fig.
10.5 (a), la branche de core-dédoute ayant été ignorée. Le suffixe M dans le stator fait référence à l’enroulement principal et EM est l’EMF induit par le stator configuré par le champ alternatif.
Le moteur est maintenant vu du point de vue de la théorie du champ rotatif. L’EMF induit résultant est composé de deux composantes égales induites par les deux champs rotatifs opposés de la même résistance, c’est-à-dire
![]()
Les impédances de magnétisation et de rotor sont divisées en deux moitiés égales connectées en série comme le montre la figure 10.5 (b); Le moteur se comporte comme deux moteurs connectés en série un correspondant à chaque champ rotatif.
Les circuits des deux moteurs de composants sont identiques à l’état stationnaire car le rotor a le même glissement par rapport à chaque champ rotatif.
Lorsque le rotor fonctionne à la vitesse n par rapport au champ avant, le glissement est s par rapport à lui et (2 – s) par rapport au champ rotatif vers l’arrière afin que le modèle de circuit modifie désormais comme sur la figure 10.5 (c).
On voit facilement à partir de cette figure que ZF / 2 ≫ ZB / 2 et donc EMF ≫ EMB, c’est-à-dire que l’effet de moteur de champ avant prédomine, créant un couple en cours d’exécution.
La nécessité pratique dicte que les deux champs rotatifs sont conçus pour avoir une force inégale dans des conditions stationnaires, ce qui fait l’auto-démarrage de l’auto-démarrage.
Cela nécessite un enroulement de plus sur le moteur appelé enroulement auxiliaire qui est en quadrature spatiale avec l’enroulement principal et comprend un plus petit nombre de virages de fil plus mince.
Cet enroulement peut être coupé du circuit une fois que le moteur a commencé, sauf en cas de moteur géré par le condensateur où il peut être lié au service d’amélioration du facteur de puissance global.
Analyse des performances:
Les performances d’un moteur à induction monophasé peuvent être obtenues par analyse du modèle de circuit du moteur donné sur la figure 10.5 (c), comme cela a été fait pour le cas d’un moteur à induction en trois phases.
Les résultats sont similaires à ceux d’un moteur à induction en trois phases car le modèle de circuit est essentiellement le même.
Les pouvoirs d’air-gap pour les champs avant et arrière sont donnés par

où IM est le courant d’enroulement principal et RF et RB sont les parties réelles des impédances du nombre complexes Z̅f et Z̅b respectivement sur la figure 10.5 (c).
Les couples produits par les deux champs peuvent être exprimés comme

où ωs = vitesse synchrone en rad / s.
Étant donné que les deux champs tournent dans des directions opposées, le couple produit par les deux s’opposent. Le couple résultant développé est donc
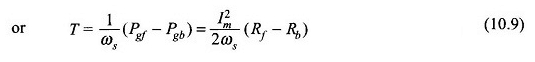
Les pertes de cuivre du rotor sont en général égales aux temps de glissement de la puissance d’air. Ainsi
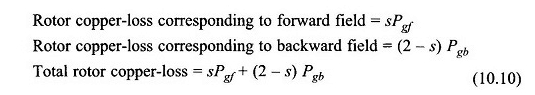
La puissance électrique convertie en forme mécanique brute est

L’équation (10.11) peut également être écrite comme
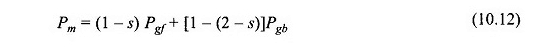
Cela implique que l’entrée d’alimentation électrique au moteur négligeant la perte de cuivre du stator est
![]()