Dynamische inductiemotormodellering:
Over het algemeen is de mechanische constante voor elke machine veel groter dan de elektrische tijdconstante. Bijgevolg kan de dynamische modellering van de inductiemotor worden vereenvoudigd door de elektrische overgangsinstelling te verwaarlozen zonder enig verlies van precisie van de resultaten.
Het inductiemotorcircuitmodel is voor een constante glijden, maar zou ook een glijdende langzaam variërend van toepassing zijn, zoals meestal het geval is in het begin van de motor.
Figuur 9.64 toont de typische koppelglijdende karakteristiek (snelheid) van dynamische inductiemotormodellering en ook het laadkoppel als een functie van het glijden (snelheid).
Elk punt op het kenmerk (TL-S) vertegenwoordigt het koppel (wrijving) dat vereist is door de belasting en de motor wanneer ze op een regelmatige snelheid werken. De motor zou alleen beginnen als t> tl en een regelmatige bedrijfssnelheid van ω0 bereiken die overeenkomt met t = tl, dat wil zeggen
Het snijpunt P van de twee koppelsnelheidseigenschappen. Het kan worden geverifieerd door de verstoringsmethode dat P een stabiel werkpunt is voor het kenmerk van de aangegeven laadsnelheid.
Als om welke reden dan ook, wordt de snelheid groter dan ω0, (t – tl) <0, de combinatie van machinaalbelasting vertraagt en keert terug naar het werkpunt. Het tegenovergestelde treedt op als de snelheid onder ω0 afneemt.

Tijdens de versnellingsperiode

waarbij j = gecombineerde traagheid van de motor en de belasting. NU

Daarom, Vgl. (9.87) aangepast aan

Integratie
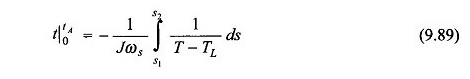
Omdat de term 1 / (t – tl) niet -lineaire integratie in de vergelijking is. (9.89) moet grafisch (of digitaal) worden uitgevoerd zoals weergegeven in figuur 9.65 voor het geval wanneer S1 = 1 en S2 = S0.
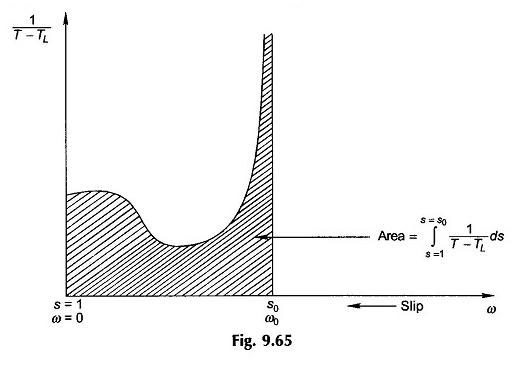
Omdat 1 / (TL) ∞ tot S0 wordt, wordt praktische integratie slechts tot 90 of 95% S0 uitgevoerd, afhankelijk van de gewenste precisie.
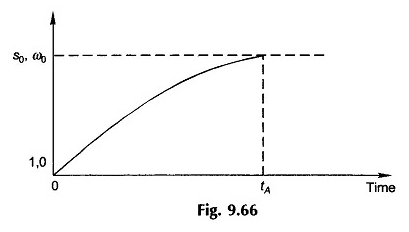
Figuur 9.66 laat zien hoe de glijdende (snelheid) in de loop van de tijd varieert tijdens de versnellingsperiode die de reguliere waarde van S0 (ω0) in de tijd bereikt, versnellingstijd. Vanwege de niet -lineariteit van (t – tl) als een functie van de verschuiving, is de schuifcurve (snelheid) in figuur 9.66 niet exponentieel.
Beginnen zonder load (tl = 0):
In dit specifieke geval wordt aangenomen dat de machine en het koppel van het laden van wrijving tl = 0.
Ervan uitgaande dat statorverliezen te verwaarlozen zijn (d.w.z. R1 = 0), is het motorkoppel verkregen uit de vergelijking. (9.22) is
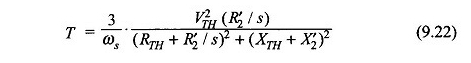
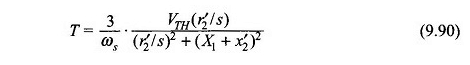
Ook van de vergelijking. (9.24)
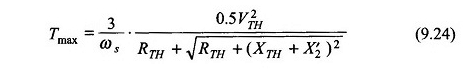

naar een verschuiving in (vergelijking (9.23)))
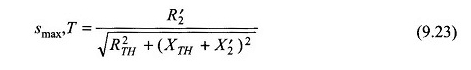

Uit vergelijkingen (9,90) en (9.91),
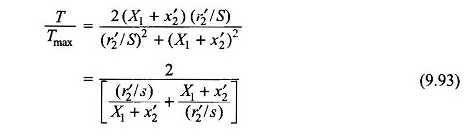
Het vervangen van de vergelijking. (9.92) in (9.93)
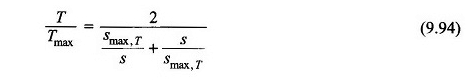
Aangezien TL wordt aangenomen dat het nul is, is het motorkoppel zelf het versnelde koppel,
Dat wil zeggen
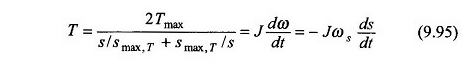
Ti om te schakelen van shift S1 naar S2 wordt verkregen tijdens de integratie van de vergelijking. (9.95) AS
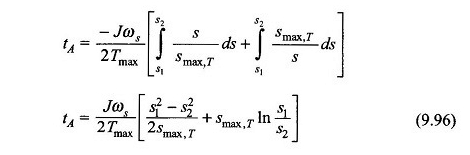
De versnellingstijd zodat de machine de reguliere start van start -UP bereikt, kan worden berekend op basis van de vergelijking. (9.96) met S1 = 1 en S2 = S, dat wil zeggen

Optimale smax, t voor minimale versnellingstijd:
Om de optimale waarde van Smax te vinden, is T voor dynamische inductiemotormodellering een minimale versnellingstijd om S2 te bereiken vanaf S1, Eq. (9.96) moet worden gedifferentieerd van smax, t en geassimileerd tot nul. Het geeft

Voor een minimale versnellingstijd voor de machine om elke slip vanaf het begin te bereiken, wordt de optimale waarde van smax, t gegeven door de vergelijking. (9.98) met S1 = 1 en S2 = S. Dus

En

Bovendien, om ons in staat te stellen de optimale waarde van rotorweerstand te berekenen om de machine te versnellen om S2 van S1, Eq te versnellen. (9.98) wordt vervangen in vergelijking. (9.92) Geef
