Przejściowa analiza silnika indukcyjnego:
Przydatność analizy przejściowych warunków pracy czytelnika, na przykład uruchamianie, hamowanie, zmiana obciążenia, zmiana prędkości itp. Jest już wyjaśniona.
Rygorystyczną analizę przejściowego działania napędu silnika indukcyjnego może być przeprowadzana tylko przez model osi DQ obejmujący długie obliczenia. Prosta metoda analityczna o zadowalającej precyzji dla większości zastosowań jest uzyskiwana przy użyciu stałych relacji pary.
Taka analiza opiera się na hipotezie, że elektryczne stałe czasowe można zaniedbać, ponieważ są bardzo małe w porównaniu z mechaniczną stałą czasową. W ten sposób możemy napisać następujące równanie do przejściowej analizy szkolenia silnika indukcyjnego:
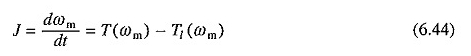
Równanie (6.44) można ocenić graficznie w celu uzyskania krzywej ωm vs t oraz strat energii w rezystancji silnika i zewnętrznego wirnika przy użyciu już wyjaśnionej metody.
Takie podejście jest ogólne i może być stosowane do każdej przejściowej analizy silnika indukcyjnego, o ile krzywe prędkości prędkości w stałej prędkości silnika [T (ω)] i obciążenie [T1 (ωM)]. Przybliżone metody analityczne przedstawiono poniżej.
Start i wtyczka:
Aby uruchomić i podłączyć działanie maszyny, moment obrotowy jest podawany przez równanie. (6.15). Zastępowanie z równania. (6.15) w (6.44)
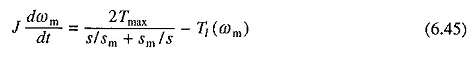
W niektórych przypadkach równanie. (6.45) będzie w formie zintegrowanej i dlatego można je rozwiązać analitycznie. Przydatne jest zbadanie stanów przejściowych do rozpoczynania operacji podczas pracy bez obciążenia. Zatem równania. (6.45) W przypadku braku ładowania

Różnicowanie równania. (6.3) daje

Zastępowanie z równania. (6.47) w (6.46) i reorganizacja warunków

τm jest mechaniczną stałą czasową silnika. Jest zdefiniowany jako czas potrzebny przez silnik, aby osiągnąć synchroniczną prędkość zatrzymania przy stałym momencie przyspieszającym równym maksymalnym momencie obrotowym silnika.
Równania. (6.48), czas wymagany do uruchomienia silnika indukcyjnego na dowolnym obciążeniu jest
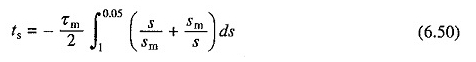
Podczas operacji bez obciążenia stanem równowagi jest osiągany, gdy s = 0. Zatem podczas rozpoczęcia -przesunięcie zmienia się z 1 na 0. Jeśli jednak (6,50) jest zintegrowane dla s = 1 do s = 0, wartość nieskończona jest uzyskiwana nieskończona wartość dla czasu rozpoczęcia.
Jak wyjaśniono, gdy końcowa prędkość jest prędkością równowagi w stanie równowagi, przejściowe są uważane za wyższy, gdy zakres prędkości 95% jest objęty. Dlatego w równaniu. (6.50) Integracja przeprowadza się od S = 1 do S = 0,05. Rozdzielczość (6.50) daje

Zatem czas rozpoczęcia zależy od SM. Czas rozpoczęcia ma minimalną wartość 1,22τm do SM = 0,4. Równania. (6.12), gdy RS jest znikomy, odporność na wirnik wymagany do uruchomienia silnika jest przynajmniej

Równania. (6.48), czas wymagany do zatrzymania według połączenia, gdy początkowo działa z synchroniczną prędkością, może być wyrażony jako
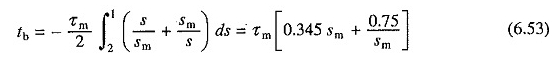
Przestój jest ponownie funkcją SM. Ma minimalną wartość 1,027τm do SM = 1,47. Odpowiednia wartość oporu dla wirnika jest
![]()
Podobnie z równania. (6.48), czas wymagany do odwrócenia prędkości poprzez podłączenie podczas wykonywania dowolnego ładunku jest podana przez
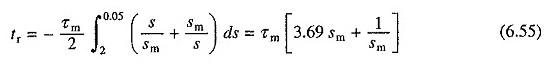
Minimalny czas odwrócenia wynosi zatem 2,88τm, a odpowiednia wartość SM wynosi 0,52. Opór wirnika wymagany do odwrócenia prędkości poprzez podłączenie minimalnego czasu jest
![]()
Obliczanie strat energii:
Następnie zaplanujmy wyrażenia utraty energii w uzwojeniach silnika w celu rozpoczęcia i łączenia. Utrata uzwojenia wirnika w celu rozpoczęcia można zapisać jako

Zastępowanie równań. (6.5) i (6.11) daje

Gdy maszyna działa pod dowolnym obciążeniem

Zastępowanie z równania. (6.47)
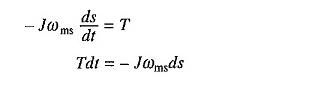
Lub
Zastępcza w (6.58) daje
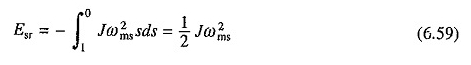
Warto zauważyć, że utrata energii uzwojenia wirnika jest równa energii kinetycznej przechowywanej w części mobilnych po zakończeniu procesu początkowego i jest niezależna od czasu odlotu lub odporności na wirnik.
Jeśli jednak opór zewnętrzny jest podłączony do obwodu wirnika, tylko część tej straty służy do podgrzewania silnika. Utrata energii w uzwojeniu stojana, zaniedbanie prądu magnetyzacji jest

Dlatego całkowita utrata uzwojenia podczas początku pod dowolnym obciążeniem jest

Postępuj w Milady, utrata uzwojenia wirnika podczas zatrzymywania się, podłączając bez obciążenia, można zapisać jako

Równanie (6.59) sugeruje, że utrata uzwojenia wirnika można zmniejszyć, gdy zaczął stosować metody oparte na zmienności prędkości synchronicznej. Na przykład rozważ silnik z układem, aby podwoić numer post.
Niech zacznie się od wyższej liczby bieguna, dla której prędkość synchroniczna wynosi ωms / 2. Następnie, od (6,59) utrata miedzi wirnika dla zmiany prędkości od 0 na ωms / 2 będzie wynosić jω2ms / 8. Teraz liczba bieguna jest obniżona. W związku z tym utrata miedzi wirnika dla zakresu prędkości ωms / 2 w ωms będzie
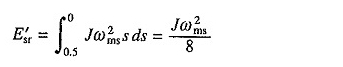
Zatem całkowite uzwojenie wirnika wynosi jω2ms / 4, co jest połową utraty miedzi, gdy nie ma żadnego postanowienia podwójnego większego poziomu bieguna.