Principe de fonctionnement du moteur à induction:
Le principe de fonctionnement du moteur d’induction de la figure 9.4 montre la vue en coupe transversale d’un moteur d’induction. Le stator est alimenté à partir d’une alimentation en trois phases en tension V / phase et fréquence f Hz. Le rotor est enroulé en 3 phases pour autant de pôles que le stator et est court-circuité. On suppose que la résistance du stator et la réactance des fuites sont tous deux négligeables pour que
![]()
où
- E1 = EMF induit par le stator / phase
- kw1 = facteur d’enroulement du stator
- NPH1 (série) = série stator tourne / phase
- Φr = flux / pôle d’air résultant
Il est vu à partir de l’équation. (9.1) Que indépendamment des conditions de charge existant sur le rotor, φr, le flux / pôle établi dans le randonnée d’air est constant, lié à la tension appliquée en vue de l’hypothèse faite.
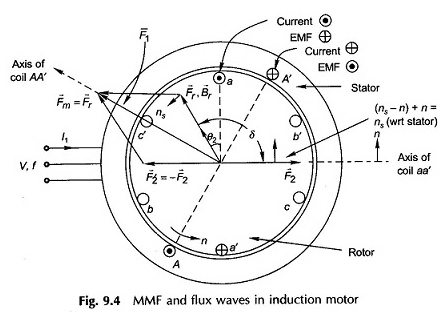
Le vecteur MMF F̅R avec le vecteur de densité de flux associé B̅R qui est responsable de la production de φR tourne à une vitesse synchrone car il est associé à des courants en 3 phases équilibrés dessinés par le stator.
La vitesse relative entre B̅r et le rotor provoque l’induction d’un motif de courant dans le rotor court-circuité.
Le couple produit par l’interaction de B̅r et les courants du rotor par la loi de Lenz tendrait à déplacer le rotor dans le sens de rotation de B̅r afin de réduire la vitesse relative.
Le moteur est donc auto-démarrant et le rotor acquiert une vitesse constante n
La figure 9.4 montre l’emplacement relatif des vecteurs F̅r, B̅r (Air-Gap MMF et densité de flux), F̅2 (Rotor MMF) dans lequel F̅R mène F̅2 par l’angle Δ = 90 ° + θ2 (action de automobile), θ2 est l’angle sous lequel les courants de rotor Rotor EMF.
L’angle θ2 est cependant très petit car la réactance du rotor est beaucoup plus petite que la résistance au rotor. Le vecteur MMF stator est alors donné par
![]()
est situé sur le diagramme vectoriel. À l’instant où le diagramme est dessiné, le stator et le rotor phase A (représenté sous forme de bobine unique) sont maximaux possibles. Le lecteur peut vérifier l’emplacement des vecteurs à partir de la phase A courants appliquant la règle de droite.
Glissement et fréquence des courants de rotor:
En référence à la figure 9.4, il est facilement observé que B̅r se déplace à vitesse (ns – n) par rapport aux conducteurs de rotor (dans le sens de B̅r). Ceci est connu sous le nom de vitesse de glissement. Le glissement est défini comme
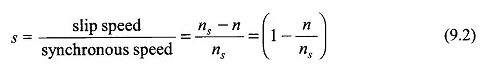
Évidemment S = 1 pour n = 0, c’est-à-dire pour le rotor stationnaire et s = 0 pour n = ns, c’est-à-dire pour le rotor fonctionnant à une vitesse synchrone.
La fréquence des courants induits dans le rotor est
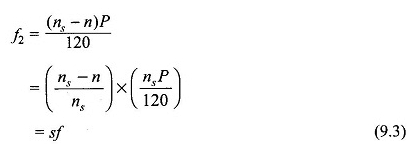
Le glissement normal à chargement complet du principe de fonctionnement du moteur d’induction est de l’ordre de 2% à 8%, de sorte que la fréquence des courants du rotor est aussi faible que 1 à 4 Hz.
Le rotor par phase EMF à S = 1 (rotor de décalage) est donné par
![]()
À n’importe quel glissement, la fréquence du rotor étant SF, l’EMF induit par le rotor se transforme en SE2. Considérez maintenant l’impédance du circuit du rotor
![]()
où
- X2 = réactance des fuites du rotor à l’arrêt (fréquence du rotor = fréquence du stator, f)
Lorsque le rotor fonctionne à Slip S, sa fréquence étant SF, son impédance se transforme en
![]()
Il est donc constaté que la fréquence des courants de rotor, son FEM induit et sa réactance varient tous en proportion directe avec le glissement. La figure 9.5 montre le circuit du rotor au glissement s. L’angle de phase du circuit est

Production de MMF et de couple du rotor:
Sur la figure 9.4 Comme le vecteur de densité de flux résultant B̅r tourne à la vitesse (ns – n) par rapport au rotor, un EMF positif maximum est induit dans la bobine de rotor aa ‘(indiqué par DOT dans le conducteur A et croix dans le conducteur A’) lorsque B̅r se trouve à 90 ° en avant de l’axe de la baisse.
Étant donné que le courant dans le rotor est à la traîne de l’EMF de θ2, le courant dans la bobine aa ‘sera maximum positif lorsque B̅r a avancé plus loin par l’angle θ2. C’est à cet instant que le vecteur MMF du rotor F̅2 se trouvera le long de l’axe de la bobine aa ‘.
Il est donc vu que B̅r (ou F̅r) se trouve à un angle δ = (90 + θ2) avant F̅2. De plus, F̅2 causé par les courants du rotor de fréquence F2 = SF tourne par rapport au conducteur du rotor à vitesse (ns – n) et à la vitesse ns.
En ce qui concerne le stator car le rotor lui-même se déplace dans la même direction à la vitesse n par rapport au stator.
Ainsi, F̅R et F̅2 se déplacent tous deux à une vitesse synchrone ns par rapport au stator et sont stationnaires les uns par rapport aux autres avec F̅r se situant devant F̅2 par angle (90 ° + θ2).
L’interaction du champ du rotor et du champ résultant crée un couple dans le sens de rotation de F̅r.
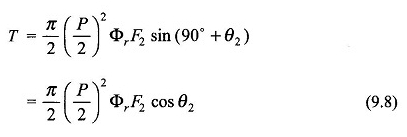
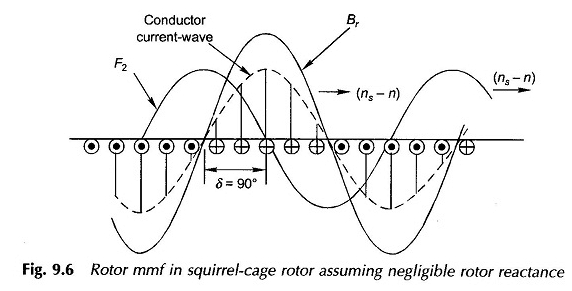
Considérez maintenant le cas du rotor d’écureuil avec des conducteurs se propage uniformément autour de la périphérie du rotor. La réaction du rotor MMF F2 est mieux visualisée à partir du diagramme développé de la Fig.
9.6 dans lequel le rotor est imaginé être stationnaire et l’onde Br – se déplaçant par rapport à elle à la vitesse de glissement (ns – n). Que la réactance du rotor soit considérée comme négligeable afin que les courants du conducteur (court-circuités) soient en phase avec le conducteur EMF s.
Le motif de courant du conducteur est donc distribué sinusoïdalement et est en phase spatiale avec Br-onde et se déplace de manière synchrone avec elle. La vague MMF du rotor est un sinusoïdal étagée avec le même nombre de pôles que le mouvement de l’onde brute avec elle.
Son fondamental (F2) représenté sur la figure 9.6 décalage de l’allège Br par 90 °. Si la réactance du rotor est désormais mise en scène, l’onde de courant du conducteur et, par conséquent, la vague MMF du rotor serait en retard par angle θ2.
Ainsi, l’angle entre l’onde Br et l’onde F2 serait (90 ° + θ2), le même que dans le rotor de la plaie.
Un rotor d’écureuil-cage réagit par conséquent de la même manière qu’un rotor de plaie, sauf que le nombre de phases n’est pas évident – on peut le considérer comme ayant autant de phases que les barres / pôles. Un rotor d’écureuil-cage peut toujours être remplacé par un rotor de plaie équivalent avec trois phases.
Il est vu à partir de l’équation. (9.8) qu’un rotor à faible réaction (faible θ2 = tan-1 jsx2 / r2) générera un couple plus grand pour φR, F2 et s donné.
Un moteur d’écureuil en cage est supérieur à cet égard par rapport à un moteur du rotor de plaie car le rotor de cage a une réactance plus faible car il n’a pas de surplomb de bobinage.
Une observation très importante qui peut être faite en principe de fonctionnement du moteur d’induction ici est que, bien que les courants du rotor aient une fréquence SF, le MMF (F2) causé par eux fonctionne à une vitesse synchrone par rapport au stator.
En d’autres termes, la réaction des courants de rotor correspond aux courants de fréquence (f) du stator qui coulent sur une structure cylindrique stationnaire équivalente placée à l’intérieur du stator à la place du rotor.
Ou, pour mettre d’une autre manière, les courants du rotor vues du stator ont la fréquence F mais ont la même valeur RMS.
Le vecteur MMF stator F̅1 est situé sur la figure 9.4 de l’équation vectorielle
![]()
De plus, F̅1 peut être divisé en composants comme
![]()
où f̅2 est en opposition à f̅2 et égal à l’ampleur et
![]()
Le courant du stator qui provoque F̅1 peut, correspondant au vecteur eq. (9.10), être divisé en composants
![]()
Ici, I̅M peut être reconnu comme un courant de magnétisation du fichier qui provoque le MMF FR résultant et le flux / pôle résultant, φR, tandis que I’2 est le composant du courant du stator qui équilibre la réaction F2 du courant du rotor I2.
La figure 9.4 montre également l’emplacement relatif de la bobine de stator aa ‘et la direction positive du courant. Cette image vectorielle instantanée tient lorsque I2 a une valeur positive maximale.
Pour que F’2 annule F2, le composant de courant du stator qui équilibre le rotor MMF doit être en phase avec le courant du rotor comme le montre le stator.
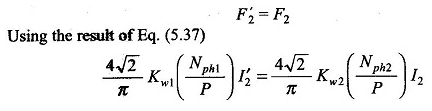

En termes d’amplitudes, F’2 est dirigée de manière opposée vers F2, pour qu’elles annulent tandis que I’2 et I2 doivent obéir à la proportionnalité de l’équation. (9.13) et doit être en phase.
De plus, par référence à la figure 9.4, on peut facilement voir que dans le stator, la direction positive de l’EMF E1 s’oppose à la direction positive de I1, tandis que dans le rotor, la direction positive de I2 est dans le sens positif de SE2. Ceci est analogue au cas du transformateur.
Avec la direction d’un courant positif dans la bobine de stator aa ‘marqué comme sur la figure 9.4 et la direction de l’axe de la bobine indiqué, la loi d’induction qui donnera une EMF positive en opposition au courant est
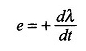
Ce principe de fonctionnement du moteur à induction a le même signe que celui utilisé dans le boîtier du transformateur de sorte que le phaseur de flux φR et le courant de magnétisation qui le crée en retard E1 de 90 °. Dans le modèle de circuit, IM serait donc dessiné par la réactance magnétisante XM à travers E1.