Modelagem de mecanismo de indução dinâmica:
Em geral, a constante mecânica para qualquer máquina é muito maior que a constante de tempo elétrico. Consequentemente, a modelagem dinâmica do mecanismo de indução pode ser simplificada negligenciando a transição elétrica sem qualquer perda de precisão dos resultados.
O modelo de circuito do motor de indução é para uma deslizamento constante, mas também se aplicaria a um deslizamento lentamente variando, como geralmente é o caso no início do motor.
A Figura 9.64 mostra a característica deslizante de torque típica (velocidade) da modelagem dinâmica do motor de indução e também o torque de carga em função do deslizamento (velocidade).
Cada ponto da característica (TL-S) representa o torque (atrito) exigido pela carga e pelo motor quando eles operam a uma velocidade regular. O motor só começaria se t> tl e atingisse uma velocidade operacional regular de ω0 que corresponde a t = tl, ou seja,
O ponto de interseção P das duas características da velocidade de torque. Pode ser verificado pelo método de perturbação que P é um ponto de operação estável para a característica da velocidade de carregamento indicada.
Se, por qualquer motivo, a velocidade se tornar maior que ω0, (t – tl) <0, a combinação de carga da máquina desacelera e retorna ao ponto de operação. O oposto ocorre se a velocidade diminuir abaixo de ω0.

Durante o período de aceleração

onde j = inércia combinada do motor e da carga. AGORA

Portanto, Eq. (9.87) modificado para

Integração
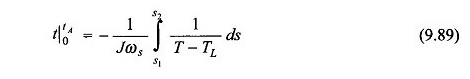
Desde então, o termo 1 / (t – tl) não é linear, integração na equação. (9.89) deve ser realizado graficamente (ou digitalmente), como mostrado na Figura 9.65, para o caso quando S1 = 1 e S2 = S0.
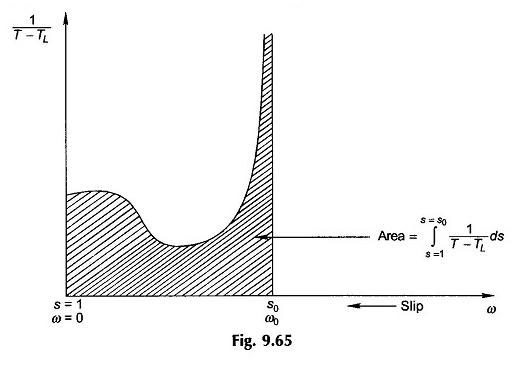
Como 1 / (tl) se torna ∞ a s0, a integração prática é realizada apenas até 90 ou 95% S0, dependendo da precisão desejada.
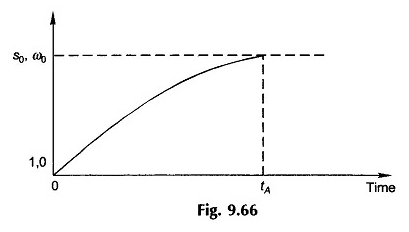
A Figura 9.66 mostra como o deslizamento (velocidade) varia ao longo do tempo durante o período de aceleração atingindo o valor regular de S0 (ω0) no tempo, tempo de aceleração. Devido à não linearidade de (t – tl) em função da mudança, a curva deslizante (velocidade) na Figura 9.66 não é exponencial.
Começando sem carga (tl = 0):
Nesse caso em particular, supõe -se que a máquina e o torque de carregar atrito tl = 0.
Supondo que as perdas do estator sejam insignificantes (ou seja, R1 = 0), o torque do motor obtido da equação. (9.22) é
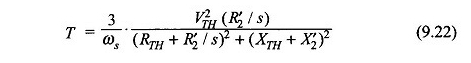
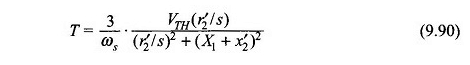
Também da equação. (9.24)
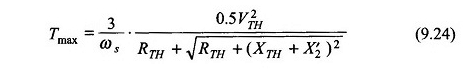

para uma mudança na (Eq. (9.23))
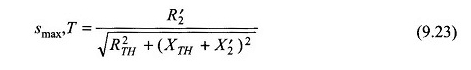

Das equações (9.90) e (9.91),
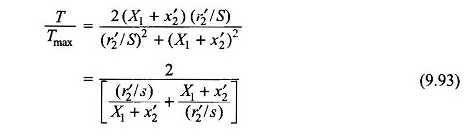
Substituindo a equação. (9.92) em (9,93)
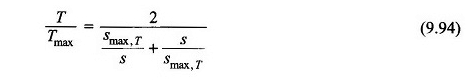
Como TL é assumido como zero, o torque do motor em si é o torque acelerado,
Isso quer dizer
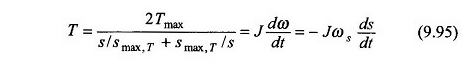
Ti para mudar do turno S1 para S2 é obtido durante a integração da equação. (9.95) AS
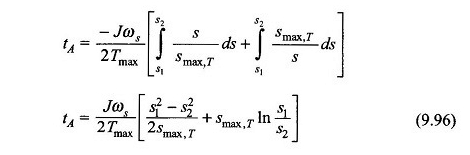
O tempo de aceleração para que a máquina atinja o início regular do início -up possa ser calculada a partir da equação. (9.96) com S1 = 1 e S2 = S, isto é,

Smax ideal, T para o tempo mínimo de aceleração:
Para encontrar o valor ideal do SMAX, T para a modelagem dinâmica de motores de indução para ter um tempo de aceleração mínima para atingir S2 de S1, Eq. (9.96) deve ser diferenciado de Smax, T e assimilado a zero. Dá

Para um tempo mínimo de aceleração para a máquina atingir qualquer deslize desde o início, o valor ideal do SMAX, t é dado pela equação. (9,98) com S1 = 1 e S2 = S. SO

E

Além disso, para nos permitir calcular o valor ideal da resistência ao rotor para acelerar a máquina para deslizar S2 de S1, Eq. (9.98) é substituído na Eq. (9.92) Give
